
 |
| AB |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 14 |
| 3 |
| 14 |
| 3 |
| 23 |
| 18 |
| 23 |
| 18 |

 |
| AB |
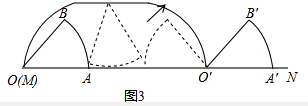
 解:计算:如图1:连接OB,
解:计算:如图1:连接OB, |
| AB |
| 60π×2 |
| 180 |
| 2 |
| 3 |
| 2 |
| 3 |

 |
| AB |
| 60π×2 |
| 180 |
| 2 |
| 3 |
| 2 |
| 3 |
| 14 |
| 3 |
| 2 |
| 3 |
| 14 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 90πR |
| 180 |
| 50π |
| 180 |
| 90πR |
| 180 |
| π |
| 2 |
| 5 |
| 18 |
| π |
| 2 |
| 23 |
| 18 |
| 23 |
| 18 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
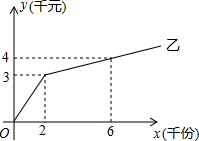 (2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表:
(2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表:| 书面材料数量x(千份) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 甲厂的印刷费用y(千元) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;
(1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;查看答案和解析>>
科目:初中数学 来源: 题型:
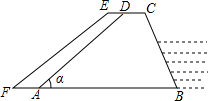 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com