
分析 (1)根据“总利润=单件利润×销售量”可得函数解析式;
(2)由(1)中相等关系列出方程求解可得;
(3)将(1)中函数解析式配方成顶点式可得函数的最值情况.
解答 解:(1)根据题意,得:W=(x-9)(-x+25)=-x2+34x-225;
(2)由题意,得:-x2+34x-225=55,
解得:x1=20,x2=14,
答:当销售单价为20或14元时,厂商每月获得的利润为55万元;
(3)∵W=-x2+34x-225=-(x-17)2+64,
∴当x=17时,W取得最大值,最大值为64,
答:当销售单价为17元时,厂商每月获得的利润最大,最大利润为64万元.
点评 本题主要考查二次函数的应用,理解题意找到蕴含的相等关系,并据此列出函数解析式和方程是解题的关键


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:选择题
| A. | -2a>-2b | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | 4-a<4-b | D. | a-4<b-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等且互相平分的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 菱形的面积等于对角线的积 | |
| D. | 平行四边形每条对角线平分一组对角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人数(人) | 2 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若AB⊥BC,则?ABCD是菱形 | B. | 若AC⊥BD,则?ABCD是正方形 | ||
| C. | 若AC=BD,则?ABCD是矩形 | D. | 若AB=AD,则?ABCD是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
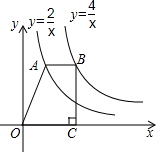 如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com