
”¾ĢāÄæ”æŃėŹÓČČ²„½ŚÄæ”°ĄŹ¶ĮÕß”±¼¤·¢ĮĖѧɜµÄŌĶĮŠĖȤ£®Ä³Š£ĪŖĀś×ćѧɜµÄŌĶĮŠčĒó£¬Óū¹ŗ½ųŅ»ÅśŃ§ÉśĻ²»¶µÄĶ¼Źé£¬Ń§Š£×éÖÆѧɜ»į³ÉŌ±Ė껜³éČ”²æ·Öѧɜ½ųŠŠĪŹ¾ķµ÷²é£¬±»µ÷²éѧɜŠė“Ó”°ĪÄŹ·Ąą”¢ÉēæĘĄą”¢Š”ĖµĄą”¢Éś»īĄą”±ÖŠŃ”Ōń×Ō¼ŗĻ²»¶µÄŅ»Ąą£¬øł¾Żµ÷²é½į¹ū»ęÖĘĮĖĶ³¼ĘĶ¼£ØĪ“Ķź³É£©£¬
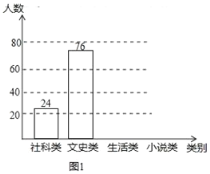
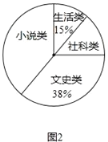
Ēėøł¾ŻĶ¼ÖŠŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©½«Ķ¼1µÄĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø2£©Ķ¼2ÖŠ”°Š”ĖµĄą”±ĖłŌŚÉČŠĪµÄŌ²ŠÄ½ĒĪŖ___________¶Č£»
£Ø3£©ČōøĆŠ£¹²ÓŠŃ§Éś2500ČĖ£¬¹Ą¼ĘøĆŠ£Ļ²»¶”°ÉēæĘĄą”±Źé¼®µÄѧɜČĖŹż£®
”¾“š°ø”æ£Ø1£©Ļź¼ū½āĪö£»£Ø2£©126£»£Ø3£©300
”¾½āĪö”æ
£Ø1£©øł¾ŻĪÄŹ·ĄąµÄČĖŹżŅŌ¼°ĪÄŹ·ĄąĖłÕ¼µÄ°Ł·Ö±Č¼“æÉĒó³ö×ÜČĖŹż£»øł¾Ż×ÜČĖŹżŅŌ¼°Éś»īĄąµÄ°Ł·Ö±Č¼“æÉĒó³öÉś»īĄąµÄČĖŹżŅŌ¼°Š”ĖµĄąµÄČĖŹż£»
£Ø2£©øł¾ŻŠ”ĖµĄąµÄ°Ł·Ö±Č¼“æÉĒó³öŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø3£©ĄūÓĆŃł±¾ÖŠĻ²»¶ÉēæĘĄąŹé¼®µÄ°Ł·Ö±ČĄ“¹Ą¼Ę×ÜĢåÖŠµÄ°Ł·Ö±Č£¬“Ó¶ųĒó³öĻ²»¶ÉēæĘĄąŹé¼®µÄѧɜČĖŹż£»
½ā£ŗ£Ø1£©”ßĻ²»¶ĪÄŹ·ĄąµÄČĖŹżĪŖ76ČĖ£¬Õ¼×ÜČĖŹżµÄ38%£¬
”ą“Ė“Īµ÷²éµÄ×ÜČĖŹżĪŖ£ŗ76”Ā38%=200ČĖ£¬
”ßĻ²»¶Éś»īĄąŹé¼®µÄČĖŹżÕ¼×ÜČĖŹżµÄ15%£¬
”ąĻ²»¶Éś»īĄąŹé¼®µÄČĖŹżĪŖ£ŗ200”Į15%=30ČĖ£¬Ļ²»¶Š”ĖµĄąŹé¼®µÄČĖŹżĪŖ£ŗ200-24-76-30=70ČĖ£¬
ČēĶ¼ĖłŹ¾£ŗ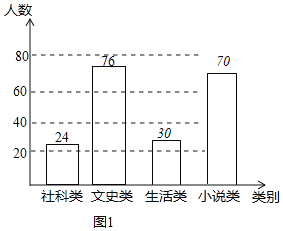
£Ø2£©”ßĻ²»¶ÉēæĘĄąŹé¼®µÄČĖŹżĪŖ£ŗ24ČĖ£¬
”ąĻ²»¶ÉēæĘĄąŹé¼®µÄČĖŹżÕ¼ĮĖ×ÜČĖŹżµÄ°Ł·Ö±ČĪŖ£ŗ![]() ”Į100%=12%£¬
”Į100%=12%£¬
”ąĻ²»¶Š”ĖµĄąŹé¼®µÄČĖŹżÕ¼ĮĖ×Ü·ÖŹżµÄ°Ł·Ö±ČĪŖ£ŗ100%-15%-38%-12%=35%£¬
”ąŠ”ĖµĄąĖłŌŚŌ²ŠÄ½ĒĪŖ£ŗ360”ć”Į35%=126”ć£¬
¹Ź“š°øĪŖ£ŗ126£»
£Ø3£©ÓÉŃł±¾Źż¾ŻæÉÖŖĻ²»¶”°ÉēæĘĄą”±Źé¼®µÄѧɜČĖŹżÕ¼ĮĖ×ÜČĖŹżµÄ12%£¬
”ąøĆŠ£¹²ÓŠŃ§Éś2500ČĖ£¬¹Ą¼ĘøĆŠ£Ļ²»¶”°ÉēæĘĄą”±Źé¼®µÄѧɜČĖŹż£ŗ2500”Į12%=300ČĖ£®


 ѧĻ°Źµ¼łŌ°µŲĻµĮŠ“š°ø
ѧĻ°Źµ¼łŌ°µŲĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
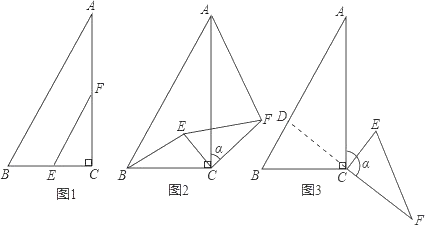
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻACB£½90”ć£¬BC£½2£¬”ĻA£½30”ć£¬µćE£¬F·Ö±šŹĒĻ߶ĪBC£¬ACµÄÖŠµć£¬Į¬½įEF£®
£Ø1£©Ļ߶ĪBEÓėAFµÄĪ»ÖĆ¹ŲĻµŹĒ”” ””£¬![]() £½”” ””£®
£½”” ””£®
£Ø2£©ČēĶ¼2£¬µ±”÷CEFČʵćCĖ³Ź±ÕėŠż×ŖaŹ±£Ø0”ć£¼a£¼180”ć£©£¬Į¬½įAF£¬BE£¬£Ø1£©ÖŠµÄ½įĀŪŹĒ·ńČŌČ»³ÉĮ¢£®Čē¹ū³ÉĮ¢£¬ĒėÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø3£©ČēĶ¼3£¬µ±”÷CEFČʵćCĖ³Ź±ÕėŠż×ŖaŹ±£Ø0”ć£¼a£¼180”ć£©£¬ŃÓ³¤FC½»ABÓŚµćD£¬Čē¹ūAD£½6©2![]() £¬ĒóŠż×Ŗ½ĒaµÄ¶ČŹż£®
£¬ĒóŠż×Ŗ½ĒaµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
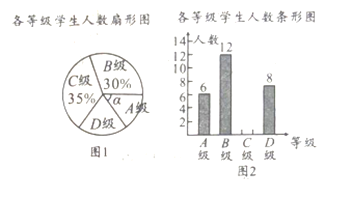
”¾ĢāÄæ”æĪŖĮĖ½ā֊ѧɜ¹ę·¶ŹéŠ“ŗŗ×ÖĒéæö£¬Ä³ŹŠÓļŃŌĪÄ×Ö¹¤×÷ĪÆŌ±»į“ÓŹŠĒų³õÖŠŌŚŠ£ÉśÖŠ³éČ”ĮĖ²æ·Öѧɜ½ųŠŠĮĖµ÷²é£¬°Ńµ÷²éµÄ½į¹ū·ÖĪŖĖÄøöµČ¼¶£ŗ![]() ¼¶£ŗÓÅŠć£»
¼¶£ŗÓÅŠć£»![]() ¼¶£ŗĮ¼ŗĆ£»
¼¶£ŗĮ¼ŗĆ£»![]() ¼¶£ŗŗĻøń£»
¼¶£ŗŗĻøń£»![]() ¼¶£ŗ²»ŗĻøń£¬²¢»ęÖĘĮĖČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ³¼ĘĶ¼ÖŠµÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
¼¶£ŗ²»ŗĻøń£¬²¢»ęÖĘĮĖČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ³¼ĘĶ¼ÖŠµÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ē󱾓Ī³éŃłµ÷²éµÄѧɜČĖŹż£»
£Ø2£©ĒóĶ¼![]() ÖŠ
ÖŠ![]() µÄ¶ČŹż£¬²¢°ŃĶ¼
µÄ¶ČŹż£¬²¢°ŃĶ¼![]() ²¹³äĶźÕū£»
²¹³äĶźÕū£»
£Ø3£©µ÷²éČĖŌ±Ļė“Ó![]() Ī»Ķ¬Ń§£Ø·Ö±š¼ĒĪŖ
Ī»Ķ¬Ń§£Ø·Ö±š¼ĒĪŖ![]() £¬ĘäÖŠ
£¬ĘäÖŠ![]() ĪŖŠ”Ć÷£©ÖŠĖ껜єŌńĮ½Ī»Ķ¬Ń§£¬²Ī¼Ó֊ѧɜĢįøߏ銓ŗŗ×ÖĖ®Ę½µÄ׳Ģø»į£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒó³öє֊Š”Ć÷µÄøÅĀŹ£®
ĪŖŠ”Ć÷£©ÖŠĖ껜єŌńĮ½Ī»Ķ¬Ń§£¬²Ī¼Ó֊ѧɜĢįøߏ銓ŗŗ×ÖĖ®Ę½µÄ׳Ģø»į£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒó³öє֊Š”Ć÷µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
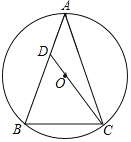
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÄŚ½ÓÓŚ”ŃO£¬AB£½AC£¬COµÄŃÓ³¤Ļß½»ABÓŚµćD£¬ČōBC£½6£¬sin”ĻBAC£½![]() £¬ŌņAC£½_____£¬CD£½_____£®
£¬ŌņAC£½_____£¬CD£½_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
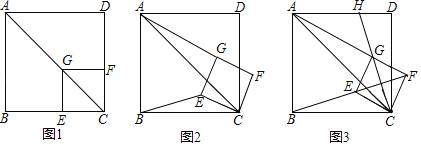
”¾ĢāÄæ”æČēĶ¼1£¬ŅŃÖŖµćGŌŚÕż·½ŠĪABCDµÄ¶Ō½ĒĻßACÉĻ£¬GE”ĶBC£¬“¹×ćĪŖµćE£¬GF”ĶCD£¬“¹×ćĪŖµćF£®
£Ø1£©Ö¤Ć÷£ŗĖıߊĪCEGFŹĒÕż·½ŠĪ£»
£Ø2£©Ģ½¾æÓėÖ¤Ć÷£ŗ
½«Õż·½ŠĪCEGFČʵćCĖ³Ź±Õė·½ĻņŠż×Ŗ¦Į½Ē£Ø0”ć£¼¦Į£¼45”ć£©£¬ČēĶ¼2ĖłŹ¾£¬ŹŌĢ½¾æĻ߶ĪAGÓėBEÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ĶŲÕ¹ÓėŌĖÓĆ£ŗ
Õż·½ŠĪCEGFČʵćCĖ³Ź±Õė·½ĻņŠż×Ŗ¦Į½Ē£Ø0”ć£¼¦Į£¼45”ć£©£¬ČēĶ¼3ĖłŹ¾£¬µ±B£¬E£¬FČżµćŌŚŅ»ĢõÖ±ĻßÉĻŹ±£¬ŃÓ³¤CG½»ADÓŚµćH£¬ČōAG£½6£¬GH£½2![]() £¬ĒóBCµÄ³¤£®
£¬ĒóBCµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=ax2©9ax+18aµÄĶ¼ĻóÓėxÖį½»ÓŚA£¬BĮ½µć£ØAŌŚBµÄ×ó²ą£©£¬Ķ¼ĻóµÄ¶„µćĪŖC£¬Ö±ĻßAC½»yÖįÓŚµćD£®
£Ø1£©Į¬½ÓBD£¬Čō”ĻBDO=”ĻCAB£¬ĒóÕāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©ŹĒ·ń“ęŌŚŅŌŌµćOĪŖ¶Ō³ĘÖįµÄ¾ŲŠĪCDEF£æČō“ęŌŚ£¬Ēó³öÕāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
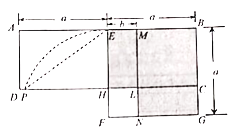
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬EĪŖABÖŠµć£¬ŅŌBEĪŖ±ß×÷Õż·½ŠĪBEFG£¬±ßEF½»CDÓŚµćH£¬ŌŚ±ßBEÉĻČ”µćMŹ¹BM£½BC£¬×÷MN”ĪBG½»CDÓŚµćL£¬½»FGÓŚµćN£®Å·¶łĄļµĆŌŚ”¶¼øŗĪŌ±¾”·ÖŠĄūÓĆøĆĶ¼½āŹĶĮĖ![]() £®ĻÖŅŌµćFĪŖŌ²ŠÄ£¬FEĪŖ°ė¾¶×÷Ō²»”½»Ļ߶ĪDHÓŚµćP£¬Į¬½įEP£¬¼Ē”÷EPHµÄĆ껿ĪŖS1£¬Ķ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖS2£®ČōµćA£¬L£¬GŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬Ōņ
£®ĻÖŅŌµćFĪŖŌ²ŠÄ£¬FEĪŖ°ė¾¶×÷Ō²»”½»Ļ߶ĪDHÓŚµćP£¬Į¬½įEP£¬¼Ē”÷EPHµÄĆ껿ĪŖS1£¬Ķ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖS2£®ČōµćA£¬L£¬GŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬Ōņ![]() µÄÖµĪŖ£Ø £©
µÄÖµĪŖ£Ø £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
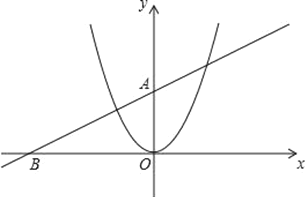
”¾ĢāÄæ”æŅŃÖŖÖ±Ļßy£½kx+b¾¹żµćA£Ø0£¬2£©£¬B£Ø©4£¬0£©ŗĶÅ×ĪļĻßy£½x2£®
£Ø1£©ĒóÖ±ĻߵĽāĪöŹ½£»
£Ø2£©½«Å×ĪļĻßy£½x2ŃŲ×ÅxÖįĻņÓŅĘ½ŅĘ£¬Ę½ŅĘŗóµÄÅ×ĪļĻ߶Ō³ĘÖį×ó²ą²æ·ÖÓėyÖį½»ÓŚµćC£¬¶Ō³ĘÖįÓŅ²ą²æ·ÖÅ×ĪļĻßÓėÖ±Ļßy£½kx+b½»ÓŚµćD£¬Į¬½ÓCD£¬µ±CD”ĪxÖįŹ±£¬ĒóĘ½ŅĘŗóµĆµ½µÄÅ×ĪļĻߵĽāĪöŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Ę½ŅĘŗóµĆµ½µÄÅ×ĪļĻߵĶŌ³ĘÖįÓėxÖį½»ÓŚµćE£¬PĪŖøĆÅ×ĪļĻßÉĻŅ»¶Æµć£¬¹żµćP×÷Å×ĪļĻ߶Ō³ĘÖįµÄ“¹Ļߣ¬“¹×ćĪŖQ£¬ŹĒ·ń“ęŌŚÕāŃłµÄµćP£¬Ź¹ŅŌµćE£¬P£¬QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷AOBĻąĖĘ£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
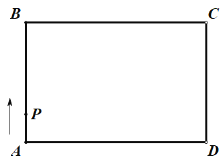
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬µć
ÖŠ£¬µć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŃŲמŲŠĪµÄ±ßĖ³Ź±Õė·½ĻņŌĖ¶ÆŅ»ÖÜ»Ųµ½µć
³ö·¢£¬ŃŲמŲŠĪµÄ±ßĖ³Ź±Õė·½ĻņŌĖ¶ÆŅ»ÖÜ»Ųµ½µć![]() £¬Ōņµć
£¬Ōņµć![]() Ī§³ÉµÄĶ¼ŠĪĆ껿
Ī§³ÉµÄĶ¼ŠĪĆ껿![]() Óėµć
Óėµć![]() ŌĖ¶ÆĀ·³Ģ
ŌĖ¶ÆĀ·³Ģ![]() Ö®¼äŠĪ³ÉµÄŗÆŹż¹ŲĻµŹ½µÄ“óÖĀĶ¼ĻóŹĒ( )
Ö®¼äŠĪ³ÉµÄŗÆŹż¹ŲĻµŹ½µÄ“óÖĀĶ¼ĻóŹĒ( )
A.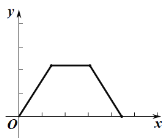 B.
B.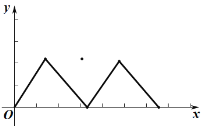
C.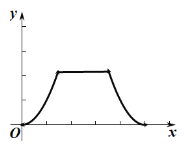 D.
D.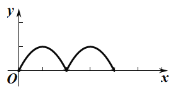
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com