
【题目】如图,等边![]() 中,
中, ![]() 是
是![]() 的角平分线,
的角平分线, ![]() 为
为![]() 上一点,以
上一点,以![]() 为一边且在
为一边且在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() .
.

(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )延长
)延长![]() 至
至![]() ,
, ![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 使
使![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )PQ=8.
)PQ=8.
【解析】试题分析:
(1)由△ABC、△DCE都是等边三角形可得:AC=BC、CD=CE,∠ACB=∠DCE=60°,从而可得∠ACD=∠BCE,这样由“SAS”即可证得:△ACD≌△BCE;
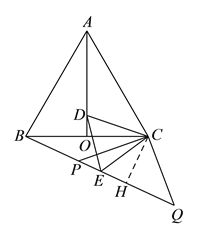
(2)由等边△ABC中,AO平分∠BAC可得∠CAD=![]() ∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=
∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=![]() BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,
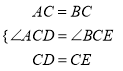 ,
,
∴![]() ≌
≌![]() .
.
(![]() )∵等边△ABC中,AO平分∠BAC,
)∵等边△ABC中,AO平分∠BAC,
∴∠CAD=![]() ∠BAC=30°.
∠BAC=30°.
如下图,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
由(![]() )知
)知![]() ≌
≌![]() ,
,
则![]() ,
,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
又∵CP=CQ,CH⊥PQ,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;(2)求证:CD是⊙P的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)计算甲、乙两人射击成绩的平均数.
(2)计算甲、乙两人的射击成绩的方差,并说明谁的成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
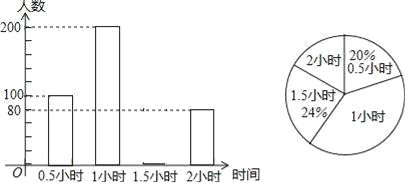
(1)求被抽样调查的学生有多少人?并补全条形统计图;
(2)该校共有1850名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:如图,AB∥OH∥CD,相邻的平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=18米,请根据上述信息求标语CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整:
已知:如图,∠ADC=∠ABC,BE、DF分别平行∠ABC、∠ADC,且∠1=∠2.
求证:∠A=∠C.
证明:因为BE、DF分别平分∠ABC、∠ADC,( ).
所以∠1=![]() ∠ABC,∠3=
∠ABC,∠3=![]() ∠ADC( ).
∠ADC( ).
因为∠ABC=∠ADC(已知),
所以∠1=∠3( ),
因为∠1=∠2(已知),
所以∠2=∠3( ).
所以 ∥ ( ).
所以∠A+∠ =180°,∠C+∠ =180°( ).
所以∠A=∠C( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
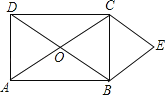
【题目】平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;
(2)当四边形ABCD是 形时,四边形OBEC是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
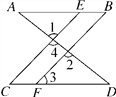
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代换),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(__________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P为∠AOB的角平分线上的一点,点D在边OA上.爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OB上取一点E,使得PE=PD,这时他发现∠OEP与∠ODP之间有一定的数量关系,请你写出∠OEP与∠ODP所有可能的数量关系是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com