
ЁОЬтФПЁПИЇжнЪае§дкељДДЪЁЮФУїГЧЪаЃЌЮЊСЫУРЛЏГЧЪаЃЌИФЩЦШЫУЧЕФОгзЁЛЗОГЃЌЮвЪаЩюШыПЊеЙТЬЛЏВЪЛЏУРЛЏЙЄГЬЃЌЭЈЙ§жВВнЁЂжжЪїЁЂаоНЈЙЋдАМАЪїеѓЪНЭЃГЕЮЛЕШЖрЯюДыЪЉЃЌЪЙГЧЧјТЬЕиУцЛ§ВЛЖЯдіМгЃЎЧыИљОнЭМжаЫљЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК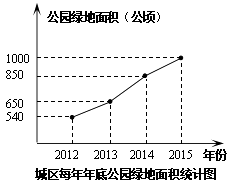
ЃЈ1ЃЉ2014ФъЕзЕФЙЋдАТЬЕиУцЛ§ЮЊЙЋЧъЃЌБШ2012ФъЕздіМгСЫЙЋЧъЃЛ
ЃЈ2ЃЉдк2013ФъЃЌ2014ФъЃЌ2015ФъетШ§ФъжаЃЌТЬЕиУцЛ§діМгзюЖрЕФЪЧФъЃЛ
ЃЈ3ЃЉЮЊТњзуГЧЪаЗЂеЙЕФашвЊЃЌМЦЛЎЕН2017ФъЕзЪЙГЧЧјЙЋдАТЬЕизмУцЛ§ДяЕН1200ЙЋЧъЃЌЪдЧѓ2017ФъЕзЙЋдАТЬЕиУцЛ§Жд2015ФъЕзЕФдіГЄТЪЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ850ЃЛ310
ЃЈ2ЃЉ2014
ЃЈ3ЃЉНтЃКгЩЬтвтПЩЕУЃЌ2017ФъЕзЙЋдАТЬЕиУцЛ§Жд2015ФъЕзЕФдіГЄТЪЪЧЃЈ1200-1000ЃЉЁТ1000=20%
ЁОНтЮіЁПНтЃКЃЈ1ЃЉЙлВьелЯпЭМЕУжЊЃЌ2014ФъЕзЕФЙЋдАТЬЕиУцЛ§ЮЊ850ЙЋЧъЃЌБШ2012ФъЕздіМгСЫ850-540=310ЙЋЧъЃЎЙЪД№АИЮЊ850ЃЛ310ЃЛЃЈ2ЃЉЭЈЙ§МЦЫу2013ФъдіМгЃК650-540=110ЙЋЧъЃЌ2014ФъдіМгЃК850-650=200ЙЋЧъЃЌ2015ФъдіМгЃК1000-850=150ЙЋЧъЃЌЙЪТЬЕиУцЛ§діМгзюЖрЕФЪЧ2014ФъЃЛ
ЃЈ1ЃЉЙлВьелЯпЭМЕУжЊЃЌ2014ФъЕзЕФЙЋдАТЬЕиУцЛ§ЮЊ850ЙЋЧъЃЌБШ2012ФъЕздіМгСЫ850-540=310ЙЋЧъЃЎЙЪД№АИЮЊ850ЃЛ310ЃЛ
ЃЈ2ЃЉЭЈЙ§МЦЫу2013ФъдіМгЃК650-540=110ЙЋЧъЃЌ2014ФъдіМгЃК850-650=200ЙЋЧъЃЌ2015ФъдіМгЃК1000-850=150ЙЋЧъЃЌЙЪТЬЕиУцЛ§діМгзюЖрЕФЪЧ2014ФъЃЛ
ЃЈ3ЃЉ2017ФъЕзЪЙГЧЧјЙЋдАТЬЕизмУцЛ§ДяЕН1200ЙЋЧъ-2015ФъЕзЙЋдАТЬЕизмУцЛ§ЕФВюдйГ§вд2015ФъЕзЙЋдАТЬЕизмУцЛ§ОЭЕУЕН2017ФъЕзЙЋдАТЬЕиУцЛ§Жд2015ФъЕзЕФдіГЄТЪ ЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЯпЖЮ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() . ЧѓзїЃКОиаЮ
. ЧѓзїЃКОиаЮ ![]() .
.
вдЯТЪЧМзЁЂввСНЭЌбЇЕФзївЕЃК
МзЃКЂй вдЕу ![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ ![]() ГЄЮЊАыОЖзїЛЁЃЛ
ГЄЮЊАыОЖзїЛЁЃЛ
Ђк вдЕу ![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ ![]() ГЄЮЊАыОЖзїЛЁЃЛ
ГЄЮЊАыОЖзїЛЁЃЛ
Ђл СНЛЁдк ![]() ЩЯЗННЛгкЕу
ЩЯЗННЛгкЕу ![]() ЃЌСЌНг
ЃЌСЌНг ![]() ЃЌ
ЃЌ ![]() .
.
ЫФБпаЮ ![]() МДЮЊЫљЧѓОиаЮ.ЃЈШчЭМЃЉ
МДЮЊЫљЧѓОиаЮ.ЃЈШчЭМЃЉ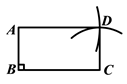
ввЃКЂй СЌНг ![]() ЃЌзїЯпЖЮ
ЃЌзїЯпЖЮ ![]() ЕФДЙжБЦНЗжЯпЃЌНЛ
ЕФДЙжБЦНЗжЯпЃЌНЛ ![]() гкЕу
гкЕу ![]() ЃЛ
ЃЛ
Ђк СЌНг ![]() ВЂбгГЄЃЌдкбгГЄЯпЩЯШЁвЛЕу
ВЂбгГЄЃЌдкбгГЄЯпЩЯШЁвЛЕу ![]() ЃЌЪЙ
ЃЌЪЙ ![]() ЃЌСЌНг
ЃЌСЌНг ![]() ЃЌ
ЃЌ ![]() .
.
ЫФБпаЮ ![]() МДЮЊЫљЧѓОиаЮ.ЃЈШчЭМЃЉ
МДЮЊЫљЧѓОиаЮ.ЃЈШчЭМЃЉ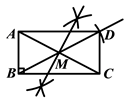
РЯЪІЫЕМзЁЂввЭЌбЇЕФзїЭМЖМе§ШЗ.
дђМзЕФзїЭМвРОнЪЧЃКЃЛ
ввЕФзїЭМвРОнЪЧЃК.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ЃЈxЉ1ЃЉ2Љ4ЕФЭМЯѓЯШЯђзѓЦНвЦ2ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ3ИіЕЅЮЛЃЌЫљЕУКЏЪ§НтЮіЪНЮЊЃЈ ЃЉ
A.y=ЃЈxЉ1ЃЉ2+1
B.y=ЃЈxЉ3ЃЉ2Љ1
C.y=ЃЈx+1ЃЉ2Љ1
D.y=ЃЈx+2ЃЉ2+3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЭЦРэе§ШЗЕФЪЧ(ЁЁЁЁ)
A. ЁпaЁЮbЃЌbЁЮcЃЌЁрcЁЮd B. ЁпaЁЮcЃЌbЁЮdЃЌЁрcЁЮd
C. ЁпaЁЮbЃЌaЁЮcЃЌЁрbЁЮc D. ЁпaЁЮbЃЌcЁЮdЃЌЁрaЁЮc
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУе§ЗНаЮгВжНАхзіШ§РтжљКазгЃЌУПИіКазггЩ3ИіГЄЗНаЮВрУцКЭ2Иіе§Ш§НЧаЮЕзУцзщГЩЃЌгВжНАхвдШчЭМСНжжЗНЗЈВУМєЃЈВУМєКѓБпНЧСЯВЛдйРћгУЃЉЃЎ
AЗНЗЈЃКМє6ИіВрУцЃЛ
BЗНЗЈЃКМє4ИіВрУцКЭ5ИіЕзУцЃЎ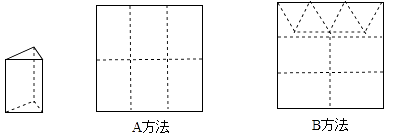
Яжга19еХгВжНАхЃЌВУМєЪБ ![]() еХгУAЗНЗЈЃЌЦфгргУBЗНЗЈЃЎ
еХгУAЗНЗЈЃЌЦфгргУBЗНЗЈЃЎ
ЃЈ1ЃЉЗжБ№ЧѓВУМєГіЕФВрУцКЭЕзУцЕФИіЪ§ЃЈгУКЌ ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉШєВУМєГіЕФВрУцКЭЕзУцЧЁКУШЋВПгУЭъЃЌЮЪФмзіЖрЩйИіКазгЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬНОПЃК
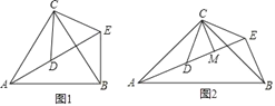
ШчЭМ1ЃЌЁїACBКЭЁїDCEОљЮЊЕШБпШ§НЧаЮЃЌЕуAЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌСЌНгBEЃЎ
ЃЈ1ЃЉжЄУїЃКAD=BEЃЛ
ЃЈ2ЃЉЧѓЁЯAEBЕФЖШЪ§ЃЎ
ЮЪЬтБфЪНЃК
ШчЭМ2ЃЌЁїACBКЭЁїDCEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=ЁЯDCE=90ЁуЃЌЕуAЁЂDЁЂEдкЭЌвЛжБЯпЩЯЃЌCMЮЊЁїDCEжаDEБпЩЯЕФИпЃЌСЌНгBEЃЎЧыЧѓГіЁЯAEBЕФЖШЪ§вдМАХаЖЯЯпЖЮCMЁЂAEЁЂBEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦпФъМЖвЛАрПЊеЙСЫвЛДЮЁАМЭФюПЙШееНељЪЄРћЦпЪЎжмФъЁБжЊЪЖОКШќЃЌОКШќЬтвЛЙВга20ЕРЬтЃЌЯТБэЪЧЦфжаЫФЮЛВЮШќбЁЪжЕФД№ЖдЬтЪ§КЭВЛД№ЛђД№ДэЬтЪ§МАЕУЗжЧщПіЃЌЧыФуИљОнБэИёжаЫљИјЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК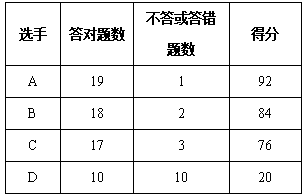
ЃЈ1ЃЉЮЪД№ЖдвЛЬтЕУЖрЩйЗжЃЌВЛД№ЛђД№ДэвЛЬтПлЖрЩйЗжЃП
ЃЈ2ЃЉвЛЮЛЭЌбЇЫЕЫћЕУСЫ75ЗжЃЌЧыЮЪПЩФмТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЪЧвЛИіГЄЮЊ ![]() ЃЌПэЮЊ
ЃЌПэЮЊ ![]() ЃЈ
ЃЈ ![]() ЃО
ЃО ![]() ЃЉЕФГЄЗНаЮЃЌгУМєЕЖбиЭМжаащЯпЃЈЖдГЦжсЃЉМєПЊЃЌАбЫќЗжГЩЫФПщаЮзДКЭДѓаЁЖМвЛбљЕФаЁГЄЗНаЮЃЌШЛКѓАДЭМЃЈ2ЃЉФЧбљЦДГЩвЛИіе§ЗНаЮЃЌдђжаМфПеЕФВПЗжЕФУцЛ§ЪЧЃЎ
ЃЉЕФГЄЗНаЮЃЌгУМєЕЖбиЭМжаащЯпЃЈЖдГЦжсЃЉМєПЊЃЌАбЫќЗжГЩЫФПщаЮзДКЭДѓаЁЖМвЛбљЕФаЁГЄЗНаЮЃЌШЛКѓАДЭМЃЈ2ЃЉФЧбљЦДГЩвЛИіе§ЗНаЮЃЌдђжаМфПеЕФВПЗжЕФУцЛ§ЪЧЃЎ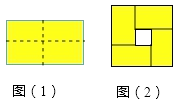
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2+mxЉ6=0ЕФвЛИіИљЮЊ2ЃЌдђm= ЃЌ СэвЛИіИљЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com