
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
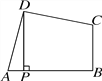
A. 3 B. 2![]() C. 3
C. 3![]() D. 3
D. 3![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的横线内.
-2.4,3,2.018,1,-0.15,0,-(-2.28),-![]() ,-|-4|.
,-|-4|.
正数:________________________;
负有理数:______________________;
整数:__________________________;
负分数:________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程 (千米)与时间 (分)关系的图象,根据图象信息,下列说法正确的是 ( )
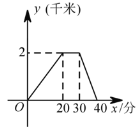
A. 小王去时的速度大于回家的速度 B. 小王去时走上坡路,回家时走下坡路
C. 小王去时所花时间少于回家所花时间 D. 小王在朋友家停留了 ![]() 分
分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队由甲乙两队组成,承包我市河东东街改造工程,规定若干天完成,已知甲单独完成这项工程所需时间比规定时间多32天,乙队单独完成这项工程所需时间比规定时间多12天,如果甲乙两队先合作20天,剩下的甲单独做,则延误两天完成,那么规定时间是多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.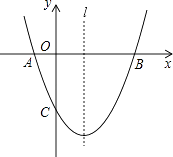
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作发现:

(1)数学活动课上,小明将已知△ABO(如图1)绕点O旋转180°得到△CDO(如图2).小明发现线段AB与CD有特殊的关系,请你写出:线段AB与CD的关系是 .
(2)连结AD(如图3),观察图形,试说明AB+AD>2AO.
(3)连结BC(如图4),观察图形,直接写出图中全等的三角形:
(写出三对即可) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约用电,某市根据每户居民每月用电量分为三档收费.第一档电价:每月用电量低于240度,每度0.4883元;第二档电价:每月用电量为240~400度,每度0.5383元;第三档电价:每月用电量为不低于400度,每度0.7883元.小灿同学对该市有1000户居民的某小区居民月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是( )

A. 本次抽样调查的样本容量为50 B. 估计该小区按第一档电价交费的居民户数最多
C. 该小区按第二档电价交费的居民有220户 D. 该小区按第三档电价交费的居民比例约为6%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com