
分析 设最后加工的两件轴的直径分别为x毫米、y毫米,根据平均数和方差公式列出方程组,解方程组可得.
解答 解:此工人最后加工的两件轴中,只有一件的直径符合要求.
设最后加工的两件轴的直径分别为x毫米,y毫米(x≤y),令x-20=m,y-20=n,取a=20,则$\overline{x′}$=$\overline{x}$-a=20-20=0.
由$\overline{x′}$=$\frac{1}{10}$×(-0.3+0.2-0.4-0.2+0.2+0.3-0.2+0+m+n)得:m+n=0.4
由S2=$\frac{1}{10}$[(-0.3)2+0.22+(-0.4)2+…+m2+n2]=0.09得:m2+n2=0.4
∴有方程组$\left\{\begin{array}{l}{m+n=0.4}\\{{m}^{2}+{n}^{2}=0.4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-0.2}\\{n=0.6}\end{array}\right.$,
∴x=-0.2+20=19.8,y=0.6+20=20.6,
因此该工人最后加工的两件轴中有一件是符合要求的(直径为19.8毫米的),一件是不符合要求的(直径为20.6毫米的).
点评 本题考查平均数、方差及解方程组的能力,平均数描述了总体的集中趋势,方差描述其波动大小,熟记平均数、方差公式是解答好本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
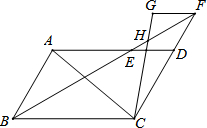 ?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.
?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
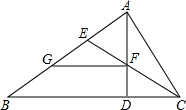 如图,Rt△ABC中,∠BAC=90°,AD是高,CE是角平分线,AE、CE交于点F.
如图,Rt△ABC中,∠BAC=90°,AD是高,CE是角平分线,AE、CE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com