
【题目】如图,在平面直角坐标系![]() ,已知四边形
,已知四边形![]() 是矩形,且
是矩形,且![]() (0,6),
(0,6),![]() (8,0),若反比例函数
(8,0),若反比例函数![]() 的图象经过线段
的图象经过线段![]() 的中点
的中点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .设直线
.设直线![]() 的解析式为
的解析式为![]() .
.

(1)求反比例函数和直线![]() 的解析式;
的解析式;
(2)求![]() 的面积:
的面积:
(3)请直接写出不等式![]() 的解集.
的解集.
【答案】(1)![]() ,
,![]() ;(2)22.5;(3)
;(2)22.5;(3)![]() 或
或![]()
【解析】
(1)由点B、D的坐标结合矩形的性质即可得出点C的坐标,由中点的性质即可得出点A的坐标,再结合反比例函数图象上点的坐标特征即可得出k值,由此即可得出反比例函数解析式;由点F的横坐标、点E的纵坐标结合反比例函数解析式即可得出点E、F的坐标,再由点E、F的坐标利用待定系数法即可求出直线EF的解析式;
(2)通过分割图形并利用三角形的面积公式即可求出结论;
(3)观察函数图象,根据两函数图象的上下关系结合交点坐标即可得出不等式的解集.
(1):![]() (0,6),
(0,6),![]() (8,0)∴
(8,0)∴![]() (8,6)∴中点
(8,6)∴中点![]() (4,3)∴
(4,3)∴![]() ∴
∴![]()
∴![]()
设![]() ,
,![]()
∴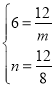 ∴
∴![]() ,
,![]() ∴
∴![]() ,
,![]()
∴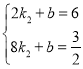 ∴
∴![]() ,
,![]() ,∴
,∴![]()
(2)![]()
=22.5
(3)根据图像可得或
![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】在下列各数![]() 中,负数的个数为m个,正数的个数为n个,绝对值最大的数为k.
中,负数的个数为m个,正数的个数为n个,绝对值最大的数为k.
(1)m= __________.n=__________.K=__________.
(2)求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,直线y=-x+6与x轴、y轴分别交于A、B两点、
直线y=![]() ax+a经过点B交x轴于点C.
ax+a经过点B交x轴于点C.
(1)求AC长;
(2)点D为线段BC上一动点,过点D作x轴平行线分别交OB、AB于点E、F,点G为AF中点,直线EG交x轴于H,设点D的横坐标为t,线段AH长为d(d≠0),求d与t之间的函数关系式;
(3)在(2)的条件下,点K为线段OA上一点,连接EK,过F作FM⊥EK,直线FM交x轴于点M,当KH=2CO,点0到直线FM的距离为![]() 时,求点D的坐标。
时,求点D的坐标。



备用图 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九宫格是一款数学游戏,起源于河图洛书,河图与洛书是我国古代流传下来的两幅神秘图案,历来被认为是河洛文化的滥觞,中华文明的源头.在如图所示的九宫格中,其每行、每列、每条对角线上三个数字之和都相等,则对于这个九宫格,下列说法错误的是( )

A.每条对角线上三个数学之和等于![]() B.三个空白方格中的数字之和等于
B.三个空白方格中的数字之和等于![]()
C.![]() 是这九个数字中最小的数D.这九个数学之和等于
是这九个数字中最小的数D.这九个数学之和等于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明玩具商店用800元购进若干套悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用1500元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元?
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于20%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校夏令营活动中,科技小组同学准备在3名老师的带领下前往国家森林公园考察,公园内有A、B两个景区可供选择,当地有甲、乙两家旅行社,可以在其中选一个两家旅行社收取的服务费用定价均为每人200元,实际收费标准如下:甲旅行社表示服务费用学生按8折优惠,带队老师免费:乙旅行社表示服务费用师生一律按照7折优惠两个景区门票定价均为每人100元,实际收费标准如下:A景区对师生均收半价,B景区规定总人数超过30人时,按4折优惠,否则按6折优惠.
(1)经核算,两家旅行社的实际服务费正好相等请你分析去哪个景区比较合算?
(2)若该学校在活动中,增加了8名学生,老师人数不变你认为去哪个景区比较合算?
(3)当有n名学生,3名老师参加时,试给出合理的方案,使得总费用最少.(总费用=服务费+门票费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c; ④4a﹣2b+c>0,其中正确有_____(填序号).
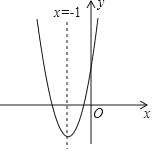
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com