【题目】某公司根据市场计划调整投资策略，对
，
两种产品进行市场调查，收集数据如表：
项目 产品 | 年固定成本 （单位：万元） | 每件成本 （单位：万元） | 每件产品销售价 （万元） | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中
是待定常数，其值是由生产的材料的市场价格决定的，变化范围是
，销售产品时需缴纳
万元的关税，其中
为生产产品的件数，假定所有产品都能在当年售出，设生产，两种产品的年利润分别为
、
（万元），写出、与之间的函数关系式，注明其自变量的取值范围．
科目：初中数学 来源： 题型：
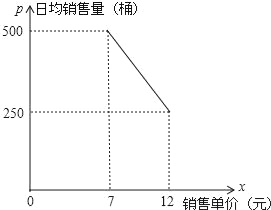
【题目】无锡市新区某桶装水经营部每天的房租、人员工资等固定成本为250元，每桶水的进价是5元，规定销售单价不得高于12元/桶，也不得低于7元/桶，调查发现日均销售量p（桶）与销售单价x（元）的函数图象如图所示．
（1）求日均销售量p（桶）与销售单价x（元）的函数关系；
（2）若该经营部希望日均获利1350元，那么销售单价是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：a、b、c均为非零实数，且a>b>c，关于x的一元二次方程
（a≠0）其中一个实数根为2。
（1）填空：4a+2b+c 0，a 0，c 0（填“>”,“<”或“=”）；
（2）若关于x的一元二次方程（a≠0）的两个实数根，满足一个根为另一个根的2倍，我们就称这样的方程为“倍根方程”，若原方程是倍根方程，则求a、c之间的关系。
（3）若a=1时，设方程的另一根为m（m≠2），在两根之间（不包含两根）的所有整数的绝对值之和是7，求b的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
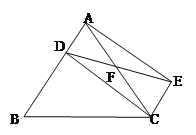
【题目】如图，D是△ABC的边AB上一点，CE∥AB，DE交AC于点F，若FA=FC．
(1)求证：四边形ADCE是平行四边形；
(2)若AE⊥EC，EF=EC=1，求四边形ADCE的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，2
，
.△ADP沿点A旋转至△ABP′，连接PP′，并延长AP与BC相交于点Q.
(1)求证：△APP′是等腰直角三角形；
(2)求∠BPQ的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某企业设计了一款工艺品，每件的成本是
元，为了合理定价，投放市场进行试销．据市场调查，销售单价是
元时，每天的销售量是件，而销售单价每降低
元，每天就可多售出
件，但要求销售单价不得低于成本．求销售单价为多少元时，每天的销售利润最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利45元，为了扩大销售、增加盈利尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出4件，若商场平均每天盈利2100元，每件衬衫应降价多少元？请完成下列问题：
（1）未降价之前，某商场衬衫的总盈利为 元．
（2）降价后，设某商场每件衬衫应降价x元，则每件衬衫盈利 元，平均每天可售出 件（用含x的代数式进行表示）
（3）请列出方程，求出x的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品x（吨），生产甲、乙两种产品获得的总利润为y（万元）．
（1）求y与x之间的函数表达式；
（2）若每生产1吨甲产品需要A原料0.25吨，每生产1吨乙产品需要A原料0.5吨．受市场影响，该厂能获得的A原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
