
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①根据表格中x与y的对应值和函数的对称性,可得出函数的对称轴;
②函数的对称轴为:x=-1,则m和![]() 对应,即可求解;
对应,即可求解;
③当x=2时y=0,根据函数的对称性,x=-4,y=0,而当-4<x<2时,y>0,即可求解;
④方程ax2+bx+c-4=0的两根,就是y=ax2+bx+c和y=4的两图像的交点的横坐标,即可求解.
解:①根据表格可得,函数的对称轴为:x=-1,此时y=![]() ,故①符合题意;
,故①符合题意;
②函数的对称轴为:x=-1,则m和![]() 对应,故②符合题意;
对应,故②符合题意;
③∵x=2,y=0,∴根据函数的对称性,x=-4,y=0,∴当-4<x<2时,y>0,故③不符合题意;
④∵ax2+bx+c-4=0,∴ax2+bx+c=4∴方程ax2+bx+c-4=0的两根,就是y=ax2+bx+c和y=4的两图像的交点的横坐标∴x1=﹣2,x2=0,故④符合题意,
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
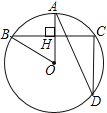
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]() .
.
(1)求证:无论![]() 取何值,这个方程总有实数根.
取何值,这个方程总有实数根.
(2)若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
(3)以方程的两根为![]() 两边,斜边为
两边,斜边为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:
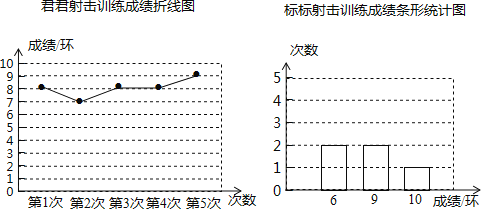
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5m,EF=0.25m,目测点D到地面的距离DG=1.5m,到旗杆的水平距离DC=20m,则旗杆的高度为( )
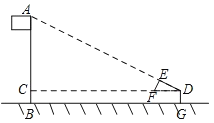
A.![]() mB.
mB.![]() m
m
C.11.5mD.10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.
(1)若方程为x2-2x=0,写出该方程的衍生点M的坐标.
(2)若关于x的一元二次方程x2-(2m+1)x+2m=0(m<0)的衍生点为M,过点M向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx-2(k-2)的图象上,若有请直接写出b,c的值,若没有说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=400,BC=600,∠ABC=45°,在△ABC内作一个内接矩形DEGF(点E、F在边BC上,点D、G分别在边AB和AC上),则矩形DEFG的对角线EG最短为_____.
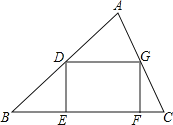
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com