
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.
【答案】
(1)9.5;10
(2)
解:乙队的平均成绩是: ![]() ×(10×4+8×2+7+9×3)=9,
×(10×4+8×2+7+9×3)=9,
则方差是: ![]() ×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)乙
【解析】解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;(2)先求出乙队的平均成绩,再根据方差公式进行计算;(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.


科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.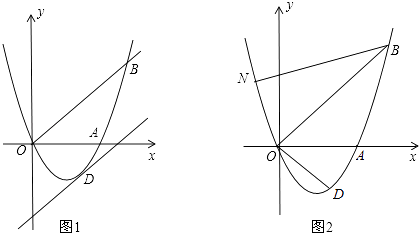
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若反比例函数y= ![]() (k≠0)的图象经过P(﹣2,3),则该函数不经过的图象的点是( )
(k≠0)的图象经过P(﹣2,3),则该函数不经过的图象的点是( )
A.(3,﹣2)
B.(1,﹣6)
C.(﹣1,6)
D.(﹣1,﹣6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形的边长为一个单位长度.已知△ABC的顶点A(-2,5)、B(-4,1)、C(2,3),将△ABC平移得到△A′B′C′,点A(a,b)对应点A′(a+3,b-4)
(1) 画出△A′B′C′并写出点B′、C′的坐标
(2) 试求线段AB在整个平移的过程中在坐标平面上扫过的面积
(3) 在x轴上存在一点P,使得S△ABP=6,则点P的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
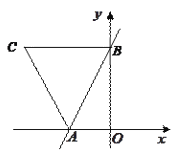
【题目】如图,已知一次函数![]() 的图像与x轴、
的图像与x轴、![]() 轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明设计了一个问题,分两步完成:
(1)已知关于x的一元一次方程![]() ,请画出数轴,并在数轴上标注a与
,请画出数轴,并在数轴上标注a与![]() 对应的点,分别记作A,B;
对应的点,分别记作A,B;
(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com