
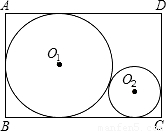
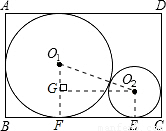
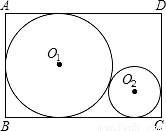
 解:(1)显然⊙O1的半径是矩形ABCD的宽的一半,即8.
解:(1)显然⊙O1的半径是矩形ABCD的宽的一半,即8.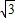 ,r2=32+16
,r2=32+16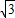 (不合题意舍去).
(不合题意舍去).

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南商丘数学考前统一模拟数学试卷(解析版) 题型:解答题
我市开发区是全国闻名的电动车生产基地,某电动车制造厂开发了一款新式电动汽车,计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装。生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车。
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
查看答案和解析>>
科目:初中数学 来源:2000年云南省昆明市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com