
����Ŀ��ij��Ʒ�����ۼ�Ϊÿ��40Ԫ��ÿ�����200��������Ʒ�������������90������ۣ��ڵ�x��1��x��49�����ڣ������ۼ۶���ǰһ������1Ԫ����������ǰһ�����2������x��50��x��90�����ڣ�������ۼ۶���90Ԫ��������Ȼ�ǽ�ǰһ�����2������֪����Ʒ�Ľ���Ϊÿ��30Ԫ����������Ʒ�ĵ�������ΪyԪ��
��1�����y��x�ĺ�����ϵʽ��
��2�����۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж����쵱������������4800Ԫ��
���𰸡���1��y=![]() ����2�����۸���Ʒ��45��ʱ��������������������Ϊ6050Ԫ����3������41�쵱������������4800Ԫ��
����2�����۸���Ʒ��45��ʱ��������������������Ϊ6050Ԫ����3������41�쵱������������4800Ԫ��
��������
��1��������������=���ۼ۩��ɱ����������������x��ȡֵ��Χ���к�����ϵʽ��
��2�����ݷֶκ������������ɷֱ�ó����ֵ���Ƚϴ�С�ɵô���
��3�����ݶ��κ���ֵ���ڻ����4800��һ�κ���ֵ���ڻ����48000���ɵò���ʽ���ⲻ��ʽ���ɵ�x�ķ�Χ���ɵô�
��1����1��x��49ʱ�������ۼ�Ϊ��40+x��Ԫ��������Ʒ��200��2x��������y=��40+x��30����200��2x��=��2x2+180x+2000��
��50��x��90ʱ�������ۼ�Ϊ90Ԫ��������Ϊ��200��2x������y=��90��30����200��2x��=��120x+12000��
��y=![]() ��
��
��2����1��x��49ʱ��y=��2x2+180x+2000=��2��x��45��2+6050���൱x=45ʱ��yȡ�����ֵ6050��
��50��x��90ʱ����y=��120x+12000֪��y��x���������С���൱x=50ʱ��yȡ�����ֵ6000��
��6050��6000�������۸���Ʒ��45��ʱ����������������������Ϊ6050Ԫ��
��3���ٵ�1��x��49ʱ����2x2+180x+2000��4800��
�����20��x��70����20��x��49��
�ڵ�50��x��90ʱ����120x+12000��4800��
�����x��60����50��x��60��
������20��x��60����ӵ�20����ֱ����60��ֹ��ÿ���������������4800Ԫ��
�ʹ���41�쵱������������4800Ԫ��


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
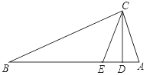
����Ŀ����ͼ������ABC�У���ACB=90����CD��AB�ڵ�D��CEƽ�֡�DCB��AB�ڵ�E��
��1����֤����AEC=��ACE��
��2������AEC=2��B��AD=2����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��������
����һ�������ӡ��м�����һ��֮颣���ȡ��룬�������ߣ������̺����������������������Ĺ�ϵ.�������Ҫ���㵽��n��ʱ���ۻ�ȡ���˶��ľ�����������������ַ���ȥ�����
����һ����n�죬������![]() ��ľ������ô�ۻ�ȡ����
��ľ������ô�ۻ�ȡ����![]() ��ľ��.
��ľ��.
����������1��ȡ����![]() ��ľ������2��ȡ����
��ľ������2��ȡ����![]() ��ľ����������n��ȡ����
��ľ����������n��ȡ����![]() ��ľ������ô�ۻ�ȡ���ˣ�
��ľ������ô�ۻ�ȡ���ˣ�![]() ��ľ��.
��ľ��.
�裺![]() ������
������
�ɢ���![]() �ã�
�ã�![]() ������
������
�٣��ڵã�![]() ��
��![]()
���϶���������ѧ�Ҹ�˹�Ĺ��£�200����ǰ����˹��������ʦ�������������⣺1+2+3+��+100=����˵������ͬѧæ�ڰ�100�����������ʱ��ʮ��ĸ�˹ȴ������ķ���Ѹ���������ȷ�Ĵ𰸣���1+100��+��2+99��+��+��50+51��=101��50=5050.
Ҳ�����������⣺��S=1+2+3+4+��+100 �٣���S=100+99+98+��+3+2+1��
��+�ڵã�2S=��1+100��+��2+99��+��3+98��+��+��100+1��=100����1+100��
��![]()
������ѧ���ķ�������������⣺
��1�����㣺![]() ��
��
��2���ҹ��Ŵ���ѧ�������㷨ͳ�ڡ������������⣺��Զ��ΡΡ���߲㣬����㱶�������������ٰ�ʮһ�����ʼ�ͷ��յ�ƣ�����˼�ǣ�һ��7����������381յ�ƣ������������е���һ���������һ���2���������Ķ��㹲�ж���յ�ƣ�
��3��ij��ѧ����ѧ������������һ��Ӧ���������Ƴ���������ѧ���ȡ�������������Ļ��ijһ�ܣ���������ļ�����Ϊ������ѧ����Ĵ𰸣���֪һ����1��1��2��1��2��4��1��2��4��8��1��2��4��8��16���������е�1����![]() ����������������
����������������![]() ��
��![]() ���ٽ�������������
���ٽ�������������![]() ��
��![]() ��
��![]() ���Դ����ƣ�����������������������N��
���Դ����ƣ�����������������������N��![]() ������һ����ǰN���Ϊ2���������ݣ������������������������������������N��ֵ.
������һ����ǰN���Ϊ2���������ݣ������������������������������������N��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
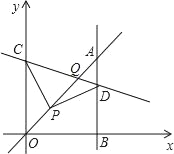
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���ֱ֪��y=x��һ��P��2��2����CΪy����һ�㣬����PC���߶�PC�Ƶ�P˳ʱ����ת90�����߶�PD������D��ֱ��AB��x�ᣬ����ΪB��ֱ��AB��ֱ��y=x���ڵ�A������CD��ֱ��CD��ֱ��y=x���ڵ�Q������OPC�ա�ADPʱ����C���������_____��Q���������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
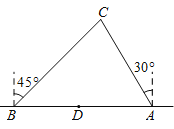
����Ŀ����ͼ�����Һ��ബ�պ���ij�������������ϵ�A��B����Ѳ����ͬʱ����һ�Ҳ���������ֻͣ��C��������AB=60��![]() +3����������B�����C�ڱ�ƫ��45�㷽������A�����C�ڱ�ƫ��30�㷽�������ں�����AB����һ����D�����AD=100������
+3����������B�����C�ڱ�ƫ��45�㷽������A�����C�ڱ�ƫ��30�㷽�������ں�����AB����һ����D�����AD=100������
��1���ֱ����AC��BC������������ţ�
��2����֪�ڵ���D��Χ80���ﷶΧ���а���Ⱥ����A�����ബ��ACǰ��C���̿���ͼ����������Σ�գ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�Ķ���A�ͶԳ������ڷ���������y=![]() ��k��0��x��0���ϣ�������ABCD�����Ϊ8����k��ֵΪ��������
��k��0��x��0���ϣ�������ABCD�����Ϊ8����k��ֵΪ��������

A. 8 B. 3![]() C. 2
C. 2![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ����ʵ��ѧУΪ�˽���꼶ѧ�����������ʲ�������������ȡ�˸��о��꼶����ѧ�����������ʲ��Գɼ���Ϊ��������A�����㣩��B�����ã���C���ϸ�D�����ϸ��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ����������ͼ������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺

��1���˴ι������˶�����ѧ����
��2��������ͳ��ͼ��������������������ͳ��ͼ�С�A����������Ӧ��Բ�ĽǵĶ�����
��3�����о��꼶����1000��ѧ���μ����������ʲ��ԣ����Ʋ��Գɼ����������ϣ������ã���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC��EB=EC��AE���ӳ��߽�BC��D����ͼ��ȫ�ȵ������ι���_____�ԣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������EBD�У�EB=ED,��C��BD�ϣ�CE=CD��BE��CE��A��CE�ӳ�����һ�㣬EA=EC.
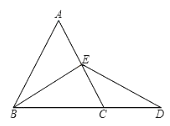
��1�����EBC�Ķ�����
��2����֤��ABCΪ�ȱ�������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com