
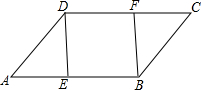
 如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
如图,在?ABCD中,E、F分别是AB、DC边上的点,且AE=CF,分析 (1)由在?ABCD中,AE=CF,可利用SAS判定△ADE≌△CBF.
(2)由在?ABCD中,且AE=CF,利用一组对边平行且相等的四边形是平行四边形,可证得四边形DEBF是平行四边形,又由∠DEB=90°,可证得四边形DEBF是矩形.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF(SAS).
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵∠DEB=90°,
∴四边形DEBF是矩形.
点评 此题考查了平行四边形的判定与性质、矩形的判定以及全等三角形的判定与性质.注意有一个角是直角的平行四边形是矩形,首先证得四边形ABCD是平行四边形是关键.


科目:初中数学 来源: 题型:填空题
 如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是13.
如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离不小于20,那么n的最小值是13.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
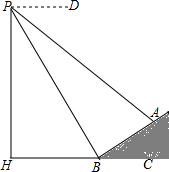 如图,数学实习小组在高500米的山腰(即PH=500米)P处进行测量,测得对面山坡上,A处的仰角为30°,对面山脚B处的俯角60°.已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
如图,数学实习小组在高500米的山腰(即PH=500米)P处进行测量,测得对面山坡上,A处的仰角为30°,对面山脚B处的俯角60°.已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
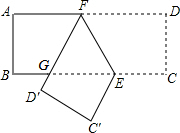 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=2$\sqrt{3}$,那么△EFG的周长为12.
如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=2$\sqrt{3}$,那么△EFG的周长为12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1<x≤2 | B. | -1<x≤2 | C. | x>-1 | D. | -1<x≤4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com