练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图：AC⊥BC，BD⊥AD，BD与AC交于E，AD=BC，求证：AE=BE．
    考点：全等三角形的判定与性质
    专题：证明题
    分析：由已知两垂直得到一对直角相等，在直角三角形ADB与直角三角形BCA中，利用HL得到两三角形全等，利用全等三角形的对应角相等得到一对角相等，利用等角对等边即可得证．
    解答：证明：∵AC⊥BC，BD⊥AD，
    ∴∠C=∠D=90°，
    在Rt△ADB和Rt△BCA中，
    AD=BC
    AB=BA
    ，
    ∴Rt△ADB≌Rt△BCA（HL），
    ∴∠ABD=∠CAB，
    则AE=BE．
    点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

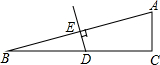    如图所示，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交AB于E，交BC于D，DB=10，那么AC=（　　）
    A、5B、10C、15D、20

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：AB=AE，AB⊥AE，AC=AF，AC⊥AF．
    （1）求证：EC=FB，EC⊥FB；
    （2）求证：S△ABC=S△AEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，
    求证：CE=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在四边形ABCD中，DC∥AB，AD=BC，BD平分∠ABC．
    （1）求证：AD=DC；
    （2）如图2，在上述条件下，若∠A=∠ABC=60°，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF．判断△DEF的形状并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

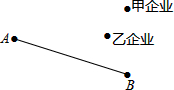    在国家“西电东送”工程中，为发展地方经济，促进甲、乙两大型企业发展，又为方便A，B两村群众，在如图所示的地理位置中，准备修一个变电站P，使变电站到A，B两村的距离相等，又要到甲、乙两企业的距离最短，请在图中作出P点的位置．（保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    画出函数y=-2x+2的图象，观察图象并回答下列问题．
    （1）方程-2x+2=0的解是多少？
    （2）当0＜y＜2时，求出对应的自变量x的取值范围．
    （3）当-1≤x＜1时，求出对应的函数值y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，CD为⊙O的直径，CD⊥AB于点F，AO⊥BC于点E，AO=2．
    （1）求∠AOD的度数；
    （2）求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    观察下列各式的计算结果
    1-
    1
    22
    =1-
    1
    4
    ═
    3
    4
    =
    1
    2
    ×
    3
    2

    1-
    1
    32
    =1-
    1
    9
    ═
    8
    9
    =
    2
    3
    ×
    4
    3

    1-
    1
    42
    =1-
    1
    16
    ═
    15
    16
    =
    3
    4
    ×
    5
    4

    1-
    1
    52
    =1-
    1
    25
    ═
    24
    25
    =
    4
    5
    ×
    6
    5

    （1）用你发现的规律填写下列式子的结果：
    1-
    1
    102
    ═
     
    ×
     
    ；
    1-
    1
    1002
    =
     
    ×
     
    ；   
    1-
    1
    20122
    =
     
    ×
     
    ；
    （2）用你发现的规律计算：（1-
    1
    22
    ）×（1-
    1
    32
    ）×（1-
    1
    42
    ）×…×（1-
    1
    20112
    ）

    查看答案和解析>>

    同步练习册答案