

 ,AK=
,AK= ,求FG的长.
,求FG的长.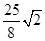
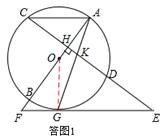
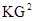 =KD·GE.理由如下:
=KD·GE.理由如下: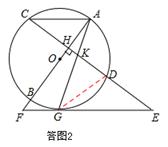
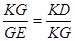 .∴KG2=KD•GE.…………………6分
.∴KG2=KD•GE.…………………6分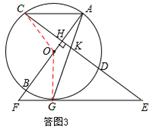
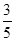 .………7分
.………7分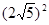 ,解得t=
,解得t=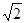 .…………………8分
.…………………8分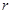 ﹣3t)2+(4t)2=
﹣3t)2+(4t)2=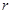 2.
2.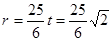 . ………………………………………………………9分
. ………………………………………………………9分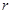 =
=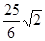 ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH= =
=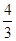 ,
,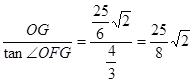 . ……………………………………10分
. ……………………………………10分

科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 是过格点A,B,C的圆弧,请完成下列问题:
是过格点A,B,C的圆弧,请完成下列问题:
 (1)用无刻度的直尺,过点B作与
(1)用无刻度的直尺,过点B作与 相切的直线l. 并写出
相切的直线l. 并写出 所在的圆的圆心P坐标;
所在的圆的圆心P坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 CD.其中正确的有 (填序号)
CD.其中正确的有 (填序号)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 BD=AB+CB,③点O是∠ADC平分线上的点,④
BD=AB+CB,③点O是∠ADC平分线上的点,④ ,上述结论中正确的编号是 .
,上述结论中正确的编号是 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
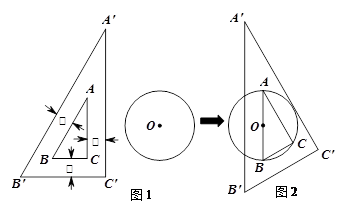
 BB′C′+
BB′C′+ CC′B′的度数。
CC′B′的度数。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com