Question

【题目】已知：点A(4，0),点B是y轴正半轴上一点，如图1，以AB为直角边作等腰直角三角形ABC.

（1）当点B坐标为(0，1)时，求点C的坐标；

（2）如图2，以OB为直角边作等腰直角△OBD，点D在第一象限，连接CD交y轴于点E.在点B运动的过程中，BE的长是否发生变化？若不变，求出BE的长；若变化，请说明理由.

Answer 1

【答案】（1）C(-1,-3)（2）在B点运动过程中，BE长保持不变，值为2

【解析】

试题（1）过C作CM⊥y轴于M，根据已知条件易证△BCM≌△ABO (AAS) ,根据全等三角形的性质可得CM=BO=1，BM=AO=4，所以OM=3，即可得C(-1,-3)；（2）在B点运动过程中，BE长保持不变，值为2，过C作CM⊥y轴于M，由（1）可知：△BCM≌△ABO，根据全等三角形的性质可得CM=BO， BM=OA=4；在判定△BCM≌△ABO (AAS) ,即可得BE=EM，从而求得BE的长.

试题解析：

（1）解：过C作CM⊥y轴于M.

∵ CM⊥y轴,∴∠BMC=∠AOB=90°,

∴∠ABO+∠BAO=90°

∵∠ABC=90°,∴∠CBM+∠ABO=90°,

∴∠CBM=∠BAO

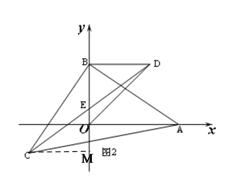
在△BCM与△ABO中 ∵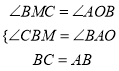

∴△BCM≌△ABO (AAS) ,

∴CM=BO=1，BM=AO=4，

∴OM=3，

∴C(-1,-3)

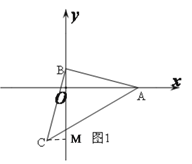
（2）在B点运动过程中，BE长保持不变，值为2，理由如下：

过C作CM⊥y轴于M，由（1）可知：△BCM≌△ABO，

∴CM=BO，BM=OA=4.

∵ △BDO是等腰直角三角形，

∴BO=BD, ∠DBO=90°,

∴CM=BD, ∠DBE=∠CME=90°,

在△DBE与△CME中，∵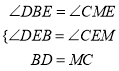

∴△DBE≌△CME(AAS)

∴BE=EM

∴BE=