
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
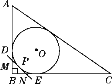
A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90°.

(1)请用圆规和直尺在AC上求作一点P,使得点P到BC边的距离等于PA的长;(保留作图痕迹,不写作法和证明)
(2)若AB=3,BC=5,求点P到BC边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是8×8的标准点阵图,直线l、m互相垂直,已知△ABC.

(1)写出△ABC的形状;
(2)分别画出△ABC关于直线l、m对称的△A1B1C1,△A2B2C2,再画出△A1B1C1关于直线m对称的△A3B3C3
(3)△A2B2C2与△A3B3C3关于哪条直线对称? (填“直线l、m”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
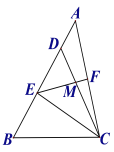
(1)求证:EF=![]() AC.
AC.
(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在正方形ABCD边AD上,连接PB,过点B作一条射线与边DC的延长线交于点 Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ,若PQ=PB+PD+3,则△PAB的面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
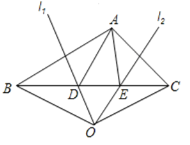
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:根据《中国铁路中长期发展规划》,预计到2020年底,我国建设城际轨道交通的公里数是客运专线的2倍。其中建设城际轨道交通约投入8000亿元,客运专线约投入3500亿元。据了解,建设每公里城际轨道交通与客运专线共需1.5亿元。预计到2020年底,我国将建设城际轨道交通和客运专线分别约多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°到点Q,将点M绕点P按逆时针方向旋转60°到点N,连接AQ,PM,PN,作直线QN.
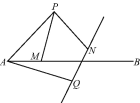
(1)求证:AM=QN.
(2)直线QN与以点P为圆心,以PN的长为半径的圆是否存在相切的情况?若存在,请求出此时AM的长,若不存在,请说明理由.
(3)当以点P为圆心,以PN的长为半径的圆经过点Q时,直接写出劣弧NQ与两条半径所围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() (
(![]() 为正整数)都在数轴上,点
为正整数)都在数轴上,点![]() 在原点
在原点![]() 的左边,且
的左边,且![]() ;点
;点![]() 在点
在点![]() 的右边,且
的右边,且![]() ;点
;点![]() 在点
在点![]() 的左边,且
的左边,且![]() ;点
;点![]() 在点
在点![]() 的右边,且
的右边,且![]() ;…,依照上述规律,点
;…,依照上述规律,点![]() 所表示的数分别为 ( )
所表示的数分别为 ( )
A.2018,-2019B.1009,-1010C.-2018,2019D.-1009,1009
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com