
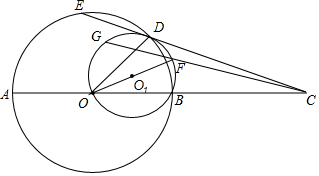
 已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆.
已知:AB是⊙O的直径,C为AB延长线上的一点,过点C作⊙O的割线,与⊙O交于D、E两点,OF是△BOD的外接圆O1的直径,连接CF并延长交⊙O1于点G.求证:O、A、E、G四点共圆. 分析 连接AD,DG,GA,GO,DB,EA,EO,由等腰三角形的性质得出OF平分∠DOB,即∠DOB=2∠DOF,由圆周角定理得出∠DAB=$\frac{1}{2}$∠DOB,得出∠DAB=∠DOF,证出∠DAB=∠DGF,得出G、A、C、D四点共圆,得出∠AGC=∠ADC,证出∠AGO=∠BDC,由圆内接四边形的性质得出∠BDC=∠EAO,由等腰三角形的性质得出∠EAO=∠AEO,证出∠AGO=∠AEO,即可得出结论.
解答 证明:连接AD,DG,GA,GO,DB,EA,EO,如图所示:
∵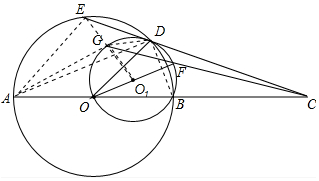 OF是等腰三角形DOB的外接圆的直径,
OF是等腰三角形DOB的外接圆的直径,
∴OF平分∠DOB,即∠DOB=2∠DOF,
又∵∠DAB=$\frac{1}{2}$∠DOB,
∴∠DAB=∠DOF,
又∵∠DGF=∠DOF,
∴∠DAB=∠DGF,
∴G、A、C、D四点共圆,
∴∠AGC=∠ADC①,
∵∠AGC=∠AGO+∠OGF=∠AGO+$\frac{π}{2}$②,∠ADC=∠ADB+∠BDC=$\frac{π}{2}$+∠BDC③,
由①②③得:∠AGO=∠BDC④,
∵B,D,E,A四点共圆,
∴∠BDC=∠EAO⑤,
又∵OA=OE,
∴∠EAO=∠AEO⑥,
由④⑤⑥得:∠AGO=∠AEO,
∴O、A、E、G四点共圆.
点评 本题是四点共圆综合题目,考查了等腰三角形的性质、圆周角定理、圆内接四边形的性质等知识;本题综合性强,难度较大,证明B,D,E,A四点共圆是解决问题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
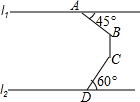 如图,在同一平面内,两条平行景观长廊l1和l2间有一条“U”形通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m,求两景观长廊间的距离(结果保留根号)
如图,在同一平面内,两条平行景观长廊l1和l2间有一条“U”形通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m,求两景观长廊间的距离(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
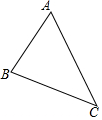 已知△ABC如图所示,求作一个△A′B′C′,使△A′B′C′≌△ABC,并写出△A′B′C′与△ABC全等的理由:SAS.(请用尺规作图)
已知△ABC如图所示,求作一个△A′B′C′,使△A′B′C′≌△ABC,并写出△A′B′C′与△ABC全等的理由:SAS.(请用尺规作图)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
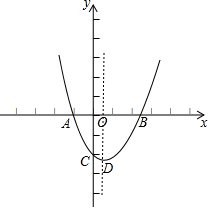 在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).
在平面直角坐标系中(如图),已知抛物线y=x2+bx+c与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
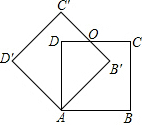 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB′C′D′,图中重合部分四边形AB′OD的面积为$\sqrt{2}$-1.
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB′C′D′,图中重合部分四边形AB′OD的面积为$\sqrt{2}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com