
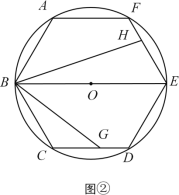
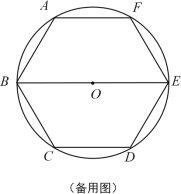
【题目】如图,已知圆O是正六边形ABCDEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x,EH=y.
(1)如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;
(2)如图②,当点G在边CD上时,试写出y关于x的函数关系式,并写出x的取值范围;
(3)联结AH、EG,如果△AFH与△DEG相似,求CG的长.

【答案】(1)∠CBG=15°;(2)![]() (
(![]() );(3)CG的长为12
);(3)CG的长为12
【解析】
(1)连接OQ,根据正六边形的特点和内角和求出∠EBC =60°,然后通过弧之间的关系得出∠BOQ=∠EOQ=90°,又因为BO=OQ,得出∠OBQ=∠BQO=45°,最后利用∠CBG=∠EBC-∠OBQ即可求出答案;
(2)在BE上截取EM=HE,连接HM,首先根据正六边形的性质得出![]() 是等边三角形,则有EM=HE=HM=y,∠HME=60°,从而有∠C=∠HMB=120°,然后通过等量代换得出∠GBC=∠HBE,由此可证明△BCG∽△BMH,则有
是等边三角形,则有EM=HE=HM=y,∠HME=60°,从而有∠C=∠HMB=120°,然后通过等量代换得出∠GBC=∠HBE,由此可证明△BCG∽△BMH,则有![]() ,即
,即![]() ,则y关于x的函数关系式可求,因为点Q在边CD上,则x的取值范围可求;
,则y关于x的函数关系式可求,因为点Q在边CD上,则x的取值范围可求;
(3)分两种情况:①当点G在边CD上时:又分当![]() 时和当
时和当![]() 时两种情况;②当点G在CD的延长线上时,同样分当
时两种情况;②当点G在CD的延长线上时,同样分当![]() 时和当
时和当![]() 时两种情况,分别建立方程求解并检验即可得出答案.
时两种情况,分别建立方程求解并检验即可得出答案.
解:(1)如图,连接OQ.
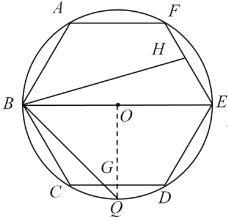
∵六边形ABCDEF是正六边形,
∴BC=DE,∠ABC=120°.
∴![]() ,∠EBC=
,∠EBC=![]() ∠ABC=60°.
∠ABC=60°.
∵点Q是![]() 的中点,
的中点,
∴![]() .
.
∴![]() ,
,
即![]() .
.
∴∠BOQ=∠EOQ,
又∵∠BOQ+∠EOQ=180°,
∴∠BOQ=∠EOQ=90°.
又∵BO=OQ,
∴∠OBQ=∠BQO=45°,
∴∠CBG=60°![]() 45°=15°.
45°=15°.
(2)如图,在BE上截取EM=HE,连接HM.
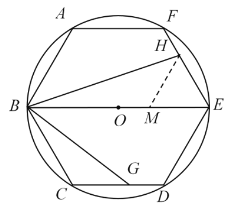
∵六边形ABCDEF是正六边形,直径BE=8,
∴BO=OE=BC=4,∠C=∠FED=120°,
∴∠FEB=![]() ∠FED=60°.
∠FED=60°.
∵EM=HE,
∴![]() 是等边三角形,
是等边三角形,
∴EM=HE=HM=y,∠HME=60°,
∴∠C=∠HMB=120°.
∵∠EBC=∠GBH=60°,
∴∠EBC![]() ∠GBE=∠GBH
∠GBE=∠GBH![]() ∠GBE,
∠GBE,
即∠GBC=∠HBE.
∴△BCG∽△BMH,
∴![]() .
.
又∵CG= x,BE=8,BC=4,
∴![]() ,
,
∴y与x的函数关系式为![]() (
(![]() ).
).
(3)如图,当点G在边CD上时.
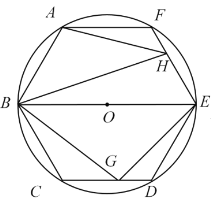
由于△AFH∽△EDG,且∠CDE=∠AFE=120°,
① 当![]() 时,
时,
∵AF=ED,
∴FH=DG,
∴![]() ,
,
即:![]() ,解分式方程得
,解分式方程得![]() .
.
经检验![]() 是原方程的解,但不符合题意舍去.
是原方程的解,但不符合题意舍去.
② 当![]() 时,
时,
即:![]() ,解分式方程得
,解分式方程得![]() .
.
经检验![]() 是原方程的解,但不符合题意舍去.
是原方程的解,但不符合题意舍去.
如图,当点G在CD的延长线上时.
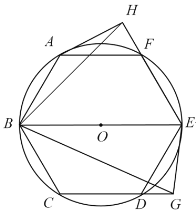
由于△AFH∽△EDG,且∠EDG=∠AFH=60°,
① 当![]() 时,
时,
∵AF=ED,
∴FH=DG
∴![]() ,
,
即:![]() ,解分式方程得
,解分式方程得![]() .
.
经检验![]() 是原方程的解,但不符合题意舍去.
是原方程的解,但不符合题意舍去.
② 当![]() 时,
时,
即:![]() ,解分式方程得
,解分式方程得![]() .
.
经检验![]() 是原方程的解,且符合题意.
是原方程的解,且符合题意.
∴综上所述,如果△AFH与△DEG相似,那么CG的长为12.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
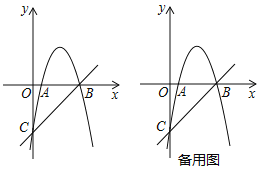
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
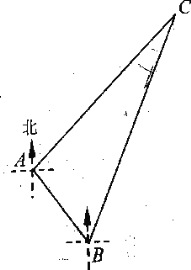
【题目】“雪龙”号考察船在某海域进行科考活动,在点 A 处测得小岛C 在它的东北方向上,它沿南偏东37°方向航行 2 海里到达点 B 处,又测得小岛C 在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点 B 处与小岛C 之间的距离.(参考数据: sin22°0.37 , cos22°0.93 , tan 22° 0.40 ,![]() 1.4 ,
1.4 ,![]() 1.7 )
1.7 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大变化,其体温(![]() )与时间(小时)之间的关系如图1所示.
)与时间(小时)之间的关系如图1所示.

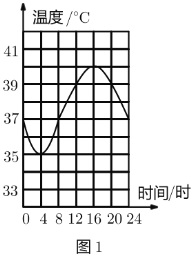
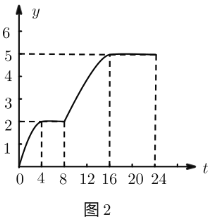
小清同学根据图1绘制了图2,则图2中的变量有可能表示的是( ).
A.骆驼在![]() 时刻的体温与0时体温的绝对差(即差的绝对值)
时刻的体温与0时体温的绝对差(即差的绝对值)
B.骆驼从0时到![]() 时刻之间的最高体温与当日最低体温的差
时刻之间的最高体温与当日最低体温的差
C.骆驼在![]() 时刻的体温与当日平均体温的绝对差
时刻的体温与当日平均体温的绝对差
D.骆驼从0时到![]() 时刻之间的体温最大值与最小值的差
时刻之间的体温最大值与最小值的差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①过三点可以确定一个圆
②直角三角形的两条直角边长分别是5和12,那么它的外接圆半径为6.5
③如果两个半径为2厘米和3厘米的圆相切,那么圆心距为5厘米
④三角形的重心到三角形三边的距离相等.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
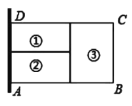
【题目】为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为![]() 的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则
的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则![]() 长为______时,能围成的矩形区域
长为______时,能围成的矩形区域![]() 的面积最大.
的面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过A(﹣1,0),B两点,且与y轴交于点C(0,3),抛物线与直线y=﹣x﹣1交于A,E两点.
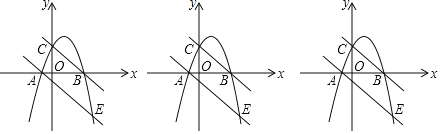
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点Q,使得△AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.
(3)P点在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
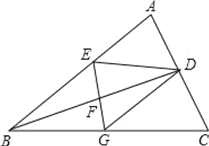
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,求GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
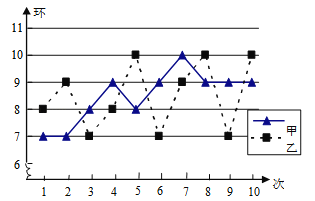
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com