
【题目】如图,在正方形![]() 中,
中,![]() ,交
,交![]() 、
、![]() 于
于![]() 、
、![]() ,交
,交![]() 于
于![]() 、
、![]() .
.
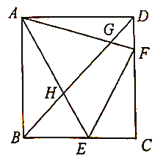
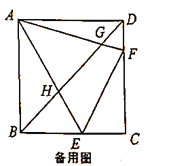
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)求证:![]() .
.
【答案】见解析
【解析】
(1)易证∠BAG=∠AHD,∠ABD=∠ADB=45°,即可证明△ABG∽△HDA,可得![]() ,即可得出结论;
,即可得出结论;
(2)首先连接AC,由正方形ABCD,∠EAF=45゜,易证得∠ACE=∠ADN=∠CAD=45°,AC=![]() AD,继而可得∠EAC=∠NAD,则可证得△EAC∽△NAD,然后由相似三角形的对应边成比例,证得结论;
AD,继而可得∠EAC=∠NAD,则可证得△EAC∽△NAD,然后由相似三角形的对应边成比例,证得结论;
(3)根据两边的比相等,且夹角相等证明△GAH∽△EAF,得![]() =
=![]() ,所以EF=
,所以EF=![]() GH.
GH.
证明:(1)∵四边形ABCD为正方形
∴∠ABD=∠ADB=45°,AB=AD,
∵∠EAF=45°
∴∠BAG=45°+∠BAH,∠AHD=45°+∠BAH,
∴∠BAG=∠AHD,
又∵∠ABD=∠ADB=45°,
∴△ABG∽△HDA,
∴![]() ,
,
∴BGDH=ABAD=AD2;
(2)如图,连接AC,
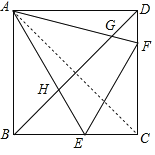
∵四边形ABCD是正方形
∴∠ACE=∠ADB=∠CAD=45°,
∴AC=![]() AD,
AD,
∵∠EAF=45°,
∴∠EAF=∠CAD,
∴∠EAF-∠CAF=∠CAD-∠CAF,
∴∠EAC=∠GAD,
∴△EAC∽△GAD,
∴![]() =
=![]() ,
,
∴CE=![]() DG;
DG;
(3)由(2)得:△EAC∽△GAD,
∴![]() =
=![]() ,
,
同理得:△AFC∽△AHB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵∠GAH=∠EAF,
∴△GAH∽△EAF,
∴![]() =
=![]() ,
,
∴EF=![]() GH.
GH.


科目:初中数学 来源: 题型:
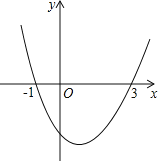
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于(-1,0),(3,0)两点,则下列说法:①abc<0;②a-b+c=0;③2a+b=0;④2a+c>0;⑤若A(x1,y1),B(x2,y2),C(x3,y3)为抛物线上三点,且-1<x1<x2<1,x3>3,则y2<y1<y3,其中正确的结论是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() .
.
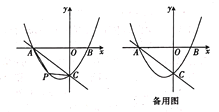
(1)求抛物线的解析式.
(2)点![]() 是抛物线上一动点,设点
是抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①若点![]() 在直线
在直线![]() 的下方,当
的下方,当![]() 的面积最大时,求
的面积最大时,求![]() 的值;
的值;
②若![]() 是以
是以![]() 为底的等腰三角形,请直接写出
为底的等腰三角形,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
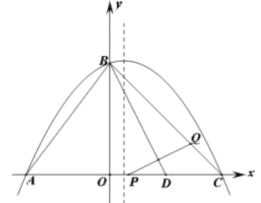
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的顶点坐标;
求这条抛物线的顶点坐标;
![]() 已知
已知![]() (点
(点![]() 在线段
在线段![]() 上),有一动点
上),有一动点![]() 从点
从点![]() 沿线段
沿线段![]() 以每秒
以每秒![]() 个单位长度的速度移动:同时另一个点
个单位长度的速度移动:同时另一个点![]() 以某一速度从点
以某一速度从点![]() 沿线段
沿线段![]() 移动,经过
移动,经过![]() 的移动,线段
的移动,线段![]() 被
被![]() 垂直平分,求
垂直平分,求![]() 的值;
的值;
![]() 在
在![]() 的情况下,抛物线的对称轴上是否存在一点
的情况下,抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的值最小?若存在,请求出点
的值最小?若存在,请求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
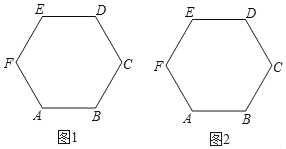
【题目】正六边形ABCDEF的边长1,请仅用无刻度的直尺按要求画图.
(1)在图1中,画出一条长度为![]() 的线段;
的线段;
(2)在图2中,画出一条长度为![]() 的线段,并说明理由.
的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.对角线相等的四边形一定是矩形
B.任意掷一枚质地均匀的硬币10次,一定有5次正面向上
C.如果有一组数据为5,3,6,4,2,那么它的中位数是6
D.“用长分别为![]() 、12cm、
、12cm、![]() 的三条线段可以围成三角形”这一事件是不可能事件
的三条线段可以围成三角形”这一事件是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
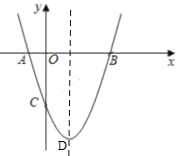
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线顶点为
,抛物线顶点为![]() ,下列四个结论:①无论
,下列四个结论:①无论![]() 取何值,
取何值,![]() 恒成立;②当
恒成立;②当![]() 时,
时,![]() 是等腰直角三角形;③若
是等腰直角三角形;③若![]() 则
则![]() ;④抛物线上有两点
;④抛物线上有两点![]() 和
和![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②④B.②③④C.①②D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com