


分析 (1)利用直角三角形斜边中线定理即可解决问题;
(2)分三种情形根据DH∥QO,可得$\frac{AD}{DB}$=$\frac{AH}{HO}$,求出AH,再利用勾股定理求解即可;
(3)由题意当等腰直角三角形的直角边为80cm时,斜边为$\sqrt{8{0}^{2}+8{0}^{2}}$≈113cm,由此即可解决问题.
解答 解:(1)∵点C是AB的中点,
∴OC=$\frac{1}{2}$AB,
∴点C的运动轨迹是以O为圆心,$\frac{1}{2}$AB长为半径的圆弧,经过的路程的$\frac{1}{4}$圆周.
故选甲.
(2)过D作DH⊥OP于H,设DH=a,在Rt△OHD中,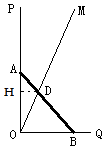
∵∠AOD=90°-600=300,
∴OD=2a,OH=$\sqrt{3}$a,
∵DH⊥OA,OQ⊥OA,
∴DH∥QO,
∴$\frac{AD}{DB}$=$\frac{AH}{HO}$,
当AD=$\frac{3}{4}$时,BD=$\frac{5}{4}$,
∴$\frac{\frac{3}{4}}{\frac{5}{4}}$=$\frac{AH}{\sqrt{3}a}$,
∴AH=$\frac{3\sqrt{3}}{5}$a,
在Rt△AHD中,
∵AH2+DH2=AD2,
∴$\frac{27}{25}$a2+a2=$\frac{9}{16}$,
解得a=$\frac{15\sqrt{13}}{104}$,OD=$\frac{30\sqrt{13}}{104}$,
当AD=1时,BD=1,
∴$\frac{1}{1}$=$\frac{AH}{\sqrt{3}a}$,
∴AH=$\sqrt{3}$a,
在Rt△AHD中,∵AH2+DH2=AD2,
∴3a2+a2=1,
解得a=$\frac{1}{2}$,OD=1,
当AD=$\frac{4}{3}$时,BD=$\frac{2}{3}$,
∴$\frac{\frac{4}{3}}{\frac{2}{3}}$=$\frac{AH}{\sqrt{3}a}$,
∴AH=2$\sqrt{3}$a,
在Rt△AHD中,∵AH2+DH2=AD2,
∴12a2+a2=$\frac{16}{9}$,
解得a=$\frac{4\sqrt{13}}{39}$,OD=$\frac{8\sqrt{13}}{39}$.
(3)由题意当等腰直角三角形的直角边为80cm时,斜边为$\sqrt{8{0}^{2}+8{0}^{2}}$≈113cm,
所以这根木棒最长可以是113cm.
故答案为113cm.
点评 本题考查相似形综合题、平行线分线段成比例定理、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,
如图,在△ABC中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )| A. | (-1,0) | B. | (1,-2) | C. | (1,1) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标平面内,点A的坐标为(0,4),点B是x轴上一点,以AB为边,在AB的一侧作正方形ABCD,对角线AC、BD相交于点E,过点C向x轴做垂线,垂足为F,点G是OF的中点,连接EG.
如图,在直角坐标平面内,点A的坐标为(0,4),点B是x轴上一点,以AB为边,在AB的一侧作正方形ABCD,对角线AC、BD相交于点E,过点C向x轴做垂线,垂足为F,点G是OF的中点,连接EG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com