
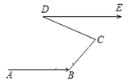
【题目】“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经 B,C,D 三点拐弯后与原来流向相同,若∠ABC =6∠CDE,∠BCD =4∠CDE,则∠CDE= _________.
【答案】![]()
【解析】
由题意可得AB∥DE,过点C作CF∥AB,则CF∥DE,由平行线的性质可得,∠BCF+∠ABC=180°,所以能用∠CDE表示出∠BCF,再由CF∥DE,所以∠CDE=∠DCF,利用∠BCD =∠BCF+∠DCF =4∠CDE,从而求得∠CDE.
解:由题意得,AB∥DE, 过点C作CF∥AB,则CF∥DE,
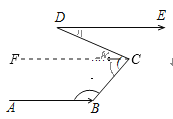
∴∠BCF+∠ABC=180°,
又∵∠ABC =6∠CDE
∴∠BCF=180°-6∠CDE,
∵∠CDE=∠DCF,
∴∠BCD=∠BCF+∠DCF=180°-6∠CDE+∠CDE=180°-5∠CDE,
而∠BCD =4∠CDE,
∴4∠CDE=180°-5∠CDE,
∴∠CDE=20°
故答案为:20°.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】为了增强学生的身体素质,西南大学附中七年级学生在每天晚自习之后进行夜跑.在学期末的体育考试中,七年级的同学们表现出很好的体育素养,并取得了良好的体育成绩.为了了解七年级学生的体育考试情况,小明抽取了部分同学的体育考试成绩进行分析,体育成绩优、良、中、差分别记为![]() 并绘制了如下两幅不完整的统计表:
并绘制了如下两幅不完整的统计表:

(1)本次调查共调查了 名学生,并补全条形统计图;
(2)扇形统计图中![]() 类所对应的扇形圆心角的度数是 度;
类所对应的扇形圆心角的度数是 度;
(3)若七年级人数为![]() 人,请你估计体育成绩优、良的总人数.
人,请你估计体育成绩优、良的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=﹣x2﹣5x+c经过点B、C,则菱形ABCD的面积为 . 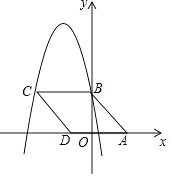
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.若AC=4,则EG2+FH2=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅会影响人们的出行,还影响着人们的健康,但是人们到底对雾霾了解多少呢?带着这种思考,某学校九年级综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了本市部分市民的观点(分四类:A类工业污染;B类汽车尾气排放;C类燃煤问题;D类其他原因.调查的每名市民只选择一种类别),并对调查结果进行录入整理,绘制了如下两幅不完整的统计图.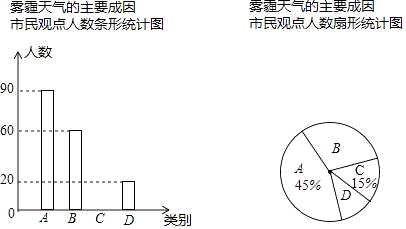
请根据图中提供的信息解答下列问题:
(1)求出本次调查的市民人数,并补全条形统计图.
(2)估计该市800万名市民中持有A、B两类看法的总人数.
(3)结合本次调查结果,请你给出一条“为减少雾霾天气发生”的合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
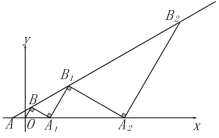
【题目】在直角坐标系中,如图所示,把∠BAO放在直角坐标系中,使射线AO与x轴重合,已知BAO=30°,OA=OB=1,过点B作BA1⊥OB交x轴于A1,过点A1做B1A1⊥BA1交直线AB于点B1,过B1作B1A2⊥B1A1交x轴于点A2,再过A2依次作垂直….则△A6B6A7的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com