
分析 先根据已知条件进行变形,利用完全平方公式可得:${a}^{4}+\frac{1}{{a}^{4}}$=194,再将所求的式子约分可得结论.
解答 解:a2-4a+1=0,
两边同时除以a,得:a-4+$\frac{1}{a}$=0,
∴a+$\frac{1}{a}$=4,
两边同时平方得:a2+2+$\frac{1}{{a}^{2}}$=16,
∴a2+$\frac{1}{{a}^{2}}$=14,
两边同时平方得:a4+2+$\frac{1}{{a}^{4}}$=196,
∴a4+$\frac{1}{{a}^{4}}$=194,
则$\frac{{a}^{8}+1}{{a}^{4}}$=a4+$\frac{1}{{a}^{4}}$=196.
点评 本题考查了分式的代入求值问题,本题有难度,不是直接将字母a的值代入,而是利用整体代入的思想,将已知条件进行变形,常采用方程两边同时除以一个数或式子的形式进行变形,或将原式变形为a2=4a-1,达到降次的目的.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1.动点P从点B出发,沿路线B-C-D作匀速运动.那么△ABP的面积S与点P的运动路程x之间的函数图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
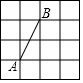 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com