
【题目】如图1,为美化校园环境,某校计划在一块长为100米,宽为60米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米﹒
(1)用含a的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽;
,求出此时通道的宽;
(3)已知某园林公司修建通道的单价是50元/米2,修建花圃的造价y(元)与花圃的修建面积S(m2)之间的函数关系如图2所示,并且通道宽a(米)的值能使关于x的方程![]() x2-ax+25a-150有两个相等的实根,并要求修建的通道的宽度不少于5米且不超过12米,如果学校决定由该公司承建此项目,请求出修建的通道和花圃的造价和为多少元?
x2-ax+25a-150有两个相等的实根,并要求修建的通道的宽度不少于5米且不超过12米,如果学校决定由该公司承建此项目,请求出修建的通道和花圃的造价和为多少元?

【答案】(1)4a2-320a+6000;(2) 通道的宽为5米;(3) 318000元.
【解析】(1)、用含a的式子先表示出花圃的长和宽后利用矩形面积公式列出式子即可;(2)、根据通道所占面积是整个长方形空地面积的![]() ,列出方程进行计算即可;(3)、根据方程有两个相等的实数根求得a的值,然后分别求得花圃和甬道的面积及造价即可.
,列出方程进行计算即可;(3)、根据方程有两个相等的实数根求得a的值,然后分别求得花圃和甬道的面积及造价即可.
(1)、由图可知,花圃的面积为(100-2a)(60-2a)=4a2-320a+6000;
(2)、由已知可列式:100×60-(100-2a)(60-2a)=![]() ×100×60,
×100×60,
解得:a1=5,a2=75(舍去),所以通道的宽为5米;
(3)、∵方程![]() x2-ax+25a-150=0有两个相等的实根, ∴△=a2-25a+150=0,解得:a1=10,a2=15,
x2-ax+25a-150=0有两个相等的实根, ∴△=a2-25a+150=0,解得:a1=10,a2=15,
∵5≤a≤12, ∴a=10. 设修建的花圃的造价为y元,y=55.625S;
当a=10时,S花圃=80×40=3200(m2);y花圃=3200×55.625=178000(元),
S通道=100×60-80×40=2800(m2);y通道=2800×50=140000(元),
造价和:178000+140000=318000(元).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离为|4﹣1|= ;表示5和﹣2两点之间的距离为|5﹣(﹣2)|=|5+2|= ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如果表示数a和﹣2的两点之间的距离是3,那么a= .
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=-![]() x,点A1的坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,则点A3的坐标为________,按此作法进行下去,点A2017的坐标为__________.
x,点A1的坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,则点A3的坐标为________,按此作法进行下去,点A2017的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算:ab=a(1﹣b).若a,b是方程x2﹣x+![]() m=0(m<0)的两根,则bb﹣aa的值为( )
m=0(m<0)的两根,则bb﹣aa的值为( )
A. 0 B. 1 C. 2 D. 与m有关
查看答案和解析>>
科目:初中数学 来源: 题型:
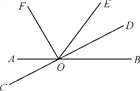
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库本周运进货物件数和运出货物件数如下表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
运进货物件数 | 5 | a | 5 | 5 | b | 5 | 5 |
运出货物件数 | 12 | 2a | 8 | 0 | b﹣5 | 5 | 10 |
(1)如果用正数表示运进货物件数,负数表示运出货物件数,请你分别表示出周二、周五当天进出货物后变化的量;
(2)若经过一周的时间,仓库货物总量相比上周末库存量减少了5件,求a的值;
(3)若本周运进货物总件数比运出货物件数的一半多15件,本周运进货物总件数比上周减少![]() ,而本周运出货物总件数比上周多
,而本周运出货物总件数比上周多![]() ,这两周内,该仓库货物共增加了3件,求a、b的值.
,这两周内,该仓库货物共增加了3件,求a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( ) 
A.旋转中心是点C
B.顺时针旋转角是90°
C.旋转中心是点B,旋转角是∠ABC
D.既可以是逆时针旋转又可以是顺时针旋转
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 为了了解东北地区初中生每天体育锻炼的时间,应采用普查的方式
B. 平均数相同的甲、乙两组数据,若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
C. 掷一枚质地均匀的硬币![]() 次,必有
次,必有![]() 次正面朝上
次正面朝上
D. 数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的中位数是
的中位数是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com