
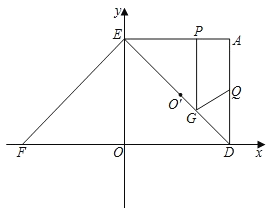
”¾ĢāÄæ”æČēĶ¼£¬µČŃüÖ±½Ē”÷OEFŌŚ×ų±źĻµÖŠ£¬ÓŠE(0£¬2)£¬F(©2£¬0)£¬½«Ö±½Ē”÷OEFČʵćEÄꏱÕėŠż×Ŗ90”ćµĆµ½”÷ADE£¬ĒŅAŌŚµŚŅ»ĻóĻŽÄŚ£¬Å×ĪļĻßy=ax2+bx+c¾¹żµćA£¬E£®ĒŅ2a+3b+5=0£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£®
£Ø2£©¹żEDµÄÖŠµćO'×÷O'B”ĶOEÓŚB£¬O'C”ĶODÓŚC£¬ĒóÖ¤£ŗOBO'CĪŖÕż·½ŠĪ£®
£Ø3£©Čē¹ūµćPÓÉEæŖŹ¼ŃŲEA±ßŅŌĆæĆė2ĄåĆ×µÄĖŁ¶ČĻņµćAŅĘ¶Æ£¬Ķ¬Ź±µćQÓɵćAŃŲAD±ßŅŌĆæĆė1ĄåĆ×µÄĖŁ¶ČĻņµćDŅĘ¶Æ£¬µ±µćPŅĘ¶Æµ½µćAŹ±£¬P£¬QĮ½µćĶ¬Ź±Ķ£Ö¹£¬ĒŅ¹żP×÷GP”ĶAE£¬½»DEÓŚµćG£¬ÉčŅĘ¶ÆµÄæŖŹ¼ŗóĪŖtĆė£®
¢ŁČōS=PQ2(ĄåĆ×)£¬ŹŌŠ“³öSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ötµÄȔֵ·¶Ī§£æ
¢Śµ±SČ”×īŠ”Ź±£¬ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćR£¬Ź¹µĆŅŌP£¬A£¬Q£¬RĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČē¹ū“ęŌŚ£¬Ēó³öRµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©Ö¤Ć÷¼ū½āĪö£»£Ø3£©¢ŁS=5t2©8t+4(0£¼t”Ü2)£»¢ŚµćRµÄ×ų±źĪŖ£ŗ(
£»£Ø2£©Ö¤Ć÷¼ū½āĪö£»£Ø3£©¢ŁS=5t2©8t+4(0£¼t”Ü2)£»¢ŚµćRµÄ×ų±źĪŖ£ŗ(![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() )£®
)£®
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅā½įŗĻŠż×ŖµÄŠŌÖŹµĆ³öAµć×ų±ź£¬ŌŁøł¾ŻEµć×ų±źµĆ³öcµÄÖµ£¬×īŗó½ųŅ»²½Ēó½ā¼“æÉ£»
£Ø2£©øł¾ŻĢāŅāĻČÖ¤Ć÷OBO'CĪŖ¾ŲŠĪ£¬ŌŁĄūÓĆČż½ĒŠĪÖŠĪ»ĻߊŌÖŹ½įŗĻĢāŅāµĆ³öO'B=OC'£¬¾Ż“Ė½ųŅ»²½Ö¤Ć÷¼“æÉ£»
£Ø3£©øł¾ŻĢāŅāĮŠ³ö¹ŲĻµŹ½¼ÓŅŌ»Æ¼ņ¼“æÉ£»¢Śøł¾ŻĢāŅā·ÖAPŹĒ±ßŹ±ŅŌ¼°PAŹĒ¶Ō½ĒĻߏ±Į½ÖÖĒéæö½ųŅ»²½·ÖĪöĢÖĀŪ¼“æÉ£®
£Ø1£©”ßE”¢F×ų±ź·Ö±šĪŖ£ŗE(0£¬2)£¬F(©2£¬0)£¬
”ąOF=OE=2£¬
øł¾ŻŠż×ŖŠŌÖŹæÉµĆ£ŗAE=OE=2£¬AD=OF=2£¬
”ąµćA×ų±źĪŖ£ŗ(2£¬2)£¬
½«µćEµÄ×ų±ź“śČėÅ×ĪļĻß±ķ“ļŹ½²¢ÕūĄķµĆ£ŗ c=2£¬
ÓÖ”ßAµć×ų±źĪŖ£ŗ(2£¬2)£¬
”ą4a+2b=0£¬
¶ų2a+3b+5=0£¬
½«ÉĻŹö¶žŹ½ĮŖĮ¢²¢½āµĆ£ŗa=![]() £¬b=-
£¬b=-![]() £¬
£¬
¹ŹÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗ![]() £»
£»
£Ø2£©ČēĶ¼ĖłŹ¾£¬
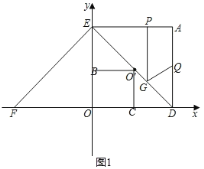
”ßO'B”ĶOE£¬O'C”ĶOD£¬”ĻEOD=90”ć£¬¹ŹOBO'CĪŖ¾ŲŠĪ£¬
ÓÖ”ßO'ŹĒEDµÄÖŠµć£¬O'B”ĶOE£¬
ŌņO'B=![]() OD£¬
OD£¬
”ßO'C”ĶOD£¬
”ąĶ¬ĄķæÉµĆ£ŗO'C=![]() OE£¬
OE£¬
”ßOE=OD£¬
”ąO'B=OC'
”ąOBO'CĪŖÕż·½ŠĪ£»
£Ø3£©¢ŁµćP”¢QµÄ×ų±ź·Ö±šĪŖ£ŗ(2t£¬2)”¢(2£¬2©t)£¬
S=PQ2=(2t©2)2+(t)2=5t2©8t+4(0£¼t”Ü2)£»
¢ŚS=5t2©8t+4(0£¼t”Ü2)£»
”ß5£¾0£¬¹ŹSÓŠ×īŠ”Öµ£¬“ĖŹ±t=![]() £¬
£¬
ŌņµćP”¢QµÄ×ų±ź·Ö±šĪŖ£ŗ(![]() £¬2)”¢(2£¬
£¬2)”¢(2£¬![]() )£¬¶ųµćA(2£¬2)£¬
)£¬¶ųµćA(2£¬2)£¬
Éč£ŗµćR(m£¬n)£¬n=![]() m2©
m2©![]() m+2£»
m+2£»
(¢ń)µ±APŹĒ±ßŹ±£¬
µćPĻņÓŅĘ½ŅĘ![]() øöµ„Ī»µĆµ½A£¬
øöµ„Ī»µĆµ½A£¬
Ķ¬ŃłµćQ(R)ĻņÓŅĘ½ŅĘ![]() øöµ„Ī»µĆµ½R(Q)£¬
øöµ„Ī»µĆµ½R(Q)£¬
¼“2![]() =m£¬½āµĆ£ŗm=
=m£¬½āµĆ£ŗm=![]() »ņ
»ņ![]() £¬
£¬
¹ŹµćR(![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() )£»
)£»
(¢ņ)µ±PAŹĒ¶Ō½ĒĻߏ±£¬
ÓÉÖŠµć¹«Ź½µĆ£ŗ2+![]() =m+2£¬
=m+2£¬
½āµĆ£ŗm=![]() £¬¹ŹµćR(
£¬¹ŹµćR(![]() £¬
£¬![]() )£»
)£»
×ŪÉĻ£¬µćRµÄ×ų±źĪŖ£ŗ(![]() £¬
£¬![]() )»ņ(
)»ņ(![]() £¬
£¬![]() )£®
)£®


 Š”ѧɜ10·ÖÖÓæŚĖć²āŹŌ100·ÖĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓæŚĖć²āŹŌ100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
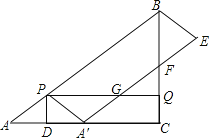
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=8cm£¬AB=10cm£®µćP“ÓµćA³ö·¢£¬ŅŌ5cm/sµÄĖŁ¶Č“ÓµćAŌĖ¶Æµ½ÖÕµćB£»Ķ¬Ź±£¬µćQ“ÓµćC³ö·¢£¬ŅŌ3cm/sµÄĖŁ¶Č“ÓµćCŌĖ¶Æµ½ÖÕµćB£¬Į¬½įPQ£»¹żµćP×÷PD”ĶAC½»ACÓŚµćD£¬½«”÷APDŃŲPD·ÕŪµĆµ½”÷A”äPD£¬ŅŌA”äPŗĶPBĪŖĮŚ±ß×÷A”äPBE£¬A”äE½»ÉäĻßBCÓŚµćF£¬½»ÉäĻßPQÓŚµćG£®ÉčA”äPBEÓėĖıߊĪPDCQÖŲµž²æ·ÖĶ¼ŠĪµÄĆ껿ĪŖScm2£¬µćPµÄŌĖ¶ÆŹ±¼äĪŖts£®
£Ø1£©µ±tĪŖŗĪÖµŹ±£¬µćA”äÓėµćCÖŲŗĻ£»
£Ø2£©ÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾QFµÄ³¤£»
£Ø3£©ĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½£»
£Ø4£©ĒėÖ±½ÓŠ“³öµ±ÉäĻßPQ½«A”äPBE·Ö³ÉµÄĮ½²æ·ÖĶ¼ŠĪµÄĆ껿֮±ČŹĒ1£ŗ3Ź±tµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
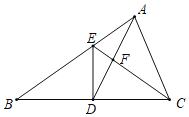
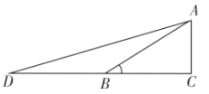
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬ADŹĒBC±ßÉĻµÄÖŠĻߣ¬ĒŅAD=AC£¬DE”ĶBC£¬DEÓėABĻą½»ÓŚµćE£¬ECÓėADĻą½»ÓŚµćF£®
(1)ĒóÖ¤£ŗ”÷ABC”×”÷FCD£»
(2)¹żµćA×÷AM”ĶBCÓŚµćM£¬ĒóDE£ŗAMµÄÖµ£»
(3)ČōS”÷FCD=5£¬BC=10£¬ĒóDEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪľߵźÄ³ÖÖĪľ߽ų¼ŪĪŖĆ漞20ŌŖ£¬ŹŠ³”µ÷²é·“Ó³£ŗµ±ŹŪ¼ŪĪŖĆ漞30ŌŖŹ±£¬Ę½¾łĆæŠĒĘŚæÉŹŪ³ö140¼ž£»¶ų°ŗĆ漞ŹŪ¼ŪÕĒ1ŌŖ£¬Ę½¾łĆæŠĒĘŚÉŁŹŪ³ö10¼ž£¬ÉčĆ漞ÕĒ¼Ū![]() ŌŖ£¬Ę½¾łĆæŠĒĘŚµÄ×ÜĄūČóĪŖ
ŌŖ£¬Ę½¾łĆæŠĒĘŚµÄ×ÜĄūČóĪŖ![]() ŌŖ£®
ŌŖ£®
£Ø1£©Š“³ö![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö×Ō±äĮæµÄȔֵ·¶Ī§£»
µÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö×Ō±äĮæµÄȔֵ·¶Ī§£»
£Ø2£©ČēŗĪ¶Ø¼Ū²ÅÄÜŹ¹ĆæŠĒĘŚµÄĄūČó×ī“ó£æĒŅĆæŠĒĘŚµÄ×ī“óĄūČóŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
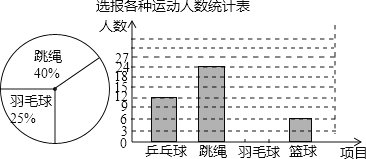
”¾ĢāÄæ”æijŠ£ĪŖĮĖĢįøßѧɜÉķĢåĖŲÖŹ£¬×éÖÆѧɜ²Ī¼ÓĘ¹ÅŅĒņ”¢ĢųÉž”¢ÓšĆ«Ēņ”¢ĄŗĒņĖÄĻīæĪĶāĢåÓż»ī¶Æ£¬ŅŖĒóѧɜøł¾Ż×Ō¼ŗµÄ°®ŗĆֻє±ØĘäÖŠŅ»Ļī£®Ń§Éś»įĖ껜³éČ”ĮĖ²æ·ÖѧɜµÄ±ØĆū±ķ£¬²¢¶Ō³éČ”µÄѧɜµÄ±ØĆūĒéæö½ųŠŠĶ³¼Ę£¬»ęÖĘĮĖĮ½·łĶ³¼ĘĶ¼(ČēĶ¼£¬²»ĶźÕū)£¬ĒėÄć½įŗĻĶ¼ÖŠµÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©³éČ”µÄ±ØĆū±ķµÄ×ÜŹżŹĒ¶ąÉŁ£æ
£Ø2£©½«Į½øöĶ³¼ĘĶ¼²¹³äĶźÕū(²»Š“¼ĘĖć¹ż³Ģ)£»
£Ø3£©øĆŠ£¹²ÓŠ200ČĖ±ØĆū²Ī¼ÓÕāĖÄĻīæĪĶāĢåÓż»ī¶Æ£¬Ń”±ØӚƫĒņµÄ“óŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCĪŖµČ±ßČż½ĒŠĪ£¬AB£½3£¬ČōµćPĪŖ”÷ABCÄŚŅ»¶Æµć£¬ĒŅĀś×ć”ĻPAB£½”ĻACP£¬ŌņĻ߶ĪPB³¤¶ČµÄ×īŠ”ÖµĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
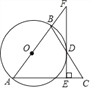
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬ŅŌABĪŖÖ±¾¶µÄ”ŃOÓė±ßBC½»ÓŚµćD£¬DE”ĶAC£¬“¹×ćĪŖE£¬½»ABµÄŃÓ³¤ĻßÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗEFŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ĻC=60”ć£¬AC=12£¬Ēó![]() µÄ³¤£®
µÄ³¤£®
£Ø3£©ČōtanC=2£¬AE=8£¬ĒóBFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ×ŪŗĻÓėŹµ¼ł£ŗ
ŌĶĮĄķ½ā£ŗŹżŃ§ŠĖȤŠ”×éŌŚĢ½¾æČēŗĪĒó![]() µÄÖµ£¬¾¹żĖ¼æ¼”¢ĢÖĀŪ”¢½»Į÷£¬µĆµ½ŅŌĻĀĖ¼Ā·£ŗ
µÄÖµ£¬¾¹żĖ¼æ¼”¢ĢÖĀŪ”¢½»Į÷£¬µĆµ½ŅŌĻĀĖ¼Ā·£ŗ
ČēĶ¼1£¬×÷![]() £¬Ź¹
£¬Ź¹![]() £¬
£¬![]() £¬ŃÓ³¤
£¬ŃÓ³¤![]() ÖĮµć
ÖĮµć![]() £¬Ź¹
£¬Ź¹![]() £¬Į¬½Ó
£¬Į¬½Ó![]() .
.
Éč![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬![]() .
.![]()
![]() .
.
Ēė½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ąą±ČĒó½ā£ŗĒó³ö![]() µÄÖµ£»
掙术
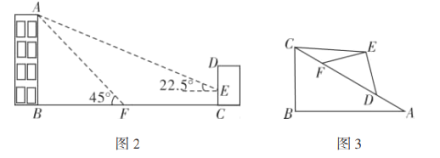
£Ø2£©ĪŹĢā½ā¾ö£ŗČēĶ¼2£¬Ä³×”Õ¬Ā„![]() µÄŗóĆęÓŠŅ»½ØÖžĪļ
µÄŗóĆęÓŠŅ»½ØÖžĪļ![]() £¬µ±¹āĻßÓėµŲĆęµÄ¼Š½ĒŹĒ
£¬µ±¹āĻßÓėµŲĆęµÄ¼Š½ĒŹĒ![]() Ź±£¬×”Õ¬ŌŚ½ØÖžĪļµÄĒ½ÉĻĮōĻĀøß
Ź±£¬×”Õ¬ŌŚ½ØÖžĪļµÄĒ½ÉĻĮōĻĀøß![]() µÄÓ°×Ó
µÄÓ°×Ó![]() £»¶ųµ±¹āĻßÓėµŲĆęµÄ¼Š½ĒŹĒ
£»¶ųµ±¹āĻßÓėµŲĆęµÄ¼Š½ĒŹĒ![]() Ź±£¬×”Õ¬Ā„¶„
Ź±£¬×”Õ¬Ā„¶„![]() ŌŚµŲĆęÉĻµÄÓ°×Ó
ŌŚµŲĆęÉĻµÄÓ°×Ó![]() ÓėĒ½½Ē
ÓėĒ½½Ē![]() ÓŠ
ÓŠ![]() µÄ¾ąĄė£Ø
µÄ¾ąĄė£Ø![]() £¬
£¬![]() £¬
£¬![]() ŌŚŅ»ĢõÖ±ĻßÉĻ£©.Ēó×”Õ¬Ā„
ŌŚŅ»ĢõÖ±ĻßÉĻ£©.Ēó×”Õ¬Ā„![]() µÄøß¶Č£Ø½į¹ū±£ĮōøłŗÅ£©£»
µÄøß¶Č£Ø½į¹ū±£ĮōøłŗÅ£©£»
£Ø3£©Ģ½¾æ·¢ĻÖ£ŗČēĶ¼3£¬Š”Ć÷ÓĆÓ²Ö½Ę¬×öĮĖĮ½øöÖ±½ĒČż½ĒŠĪ£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £»ŌŚ
£»ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() .Ėū½«
.Ėū½«![]() µÄŠ±±ß
µÄŠ±±ß![]() Óė
Óė![]() µÄŠ±±ß
µÄŠ±±ß![]() ÖŲŗĻŌŚŅ»Ęš£¬²¢½«
ÖŲŗĻŌŚŅ»Ęš£¬²¢½«![]() ŃŲ
ŃŲ![]() ·½ĻņŅʶÆ.ŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬
·½ĻņŅʶÆ.ŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬![]() £¬
£¬![]() Į½µćŹ¼ÖÕŌŚ
Į½µćŹ¼ÖÕŌŚ![]() ±ßÉĻ£ØŅʶÆæŖŹ¼Ź±µć
±ßÉĻ£ØŅʶÆæŖŹ¼Ź±µć![]() Óėµć
Óėµć![]() ÖŲŗĻ£©.Ģ½¾æŌŚ
ÖŲŗĻ£©.Ģ½¾æŌŚ![]() ŅĘ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³øöĪ»ÖĆ£¬Ź¹µĆ
ŅĘ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³øöĪ»ÖĆ£¬Ź¹µĆ![]() £æČē¹ū“ęŌŚ£¬Ö±½ÓŠ“³ö
£æČē¹ū“ęŌŚ£¬Ö±½ÓŠ“³ö![]() µÄ³¤¶Č£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄ³¤¶Č£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬AB=3£¬BC=4£¬¶ÆµćP“ÓAµć³ö·¢£¬°“A”śB”śCµÄ·½ĻņŌŚABŗĶBCÉĻŅĘ¶Æ£¬¼ĒPA=x£¬µćDµ½Ö±ĻßPAµÄ¾ąĄėĪŖy£¬Ōņy¹ŲÓŚxµÄŗÆŹżĶ¼Ļó“óÖĀŹĒ£Ø £©

A. B.
B.
C. D.
D.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com