
分析 (1)直接根据一元二次方程的定义以及根的判别式意义求出m的取值范围;
(2)首先求出一元二次方程的两根,一根为1,一根为$1+\frac{2}{m-1}$,只需要求出$\frac{2}{m-1}$是正整数时m的值即可.
解答 解:(1)根据题意得m≠1,
△=(-2m)2-4(m-1)(m+1)=4,
即m的取值范围是m≠1;
(2)∴x1=$\frac{2m-2}{{2({m-1})}}=1$,
x2=$\frac{2m+2}{{2({m-1})}}$=$\frac{m+1}{m-1}$
x2=$\frac{m+1}{m-1}$=$1+\frac{2}{m-1}$,
∵方程的两个根都是正整数,
∴$\frac{2}{m-1}$是正整数,
∴m-1=1或2
∴m=2或3.
点评 本题主要考查了根的判别式的知识,解答本题的关键是掌握根的判别式与根的个数的关系,此题难度不大.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
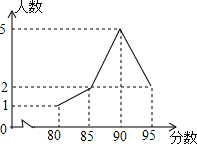 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )| A. | 众数是90分 | B. | 中位数是90分 | C. | 平均数是90分 | D. | 极差是15分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).
如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D三点在同一直线上,∠D=42°,当∠B的度数是多少时,EC∥FD?说明理由.
如图,△ABC中,∠A=46°,CE是∠ACB的平分线,B、C、D三点在同一直线上,∠D=42°,当∠B的度数是多少时,EC∥FD?说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com