
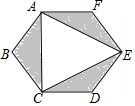
 如图,正六边形ABCDEF是一块绿化带,阴影部分都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为$\frac{1}{2}$.
如图,正六边形ABCDEF是一块绿化带,阴影部分都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为$\frac{1}{2}$. 分析 根据正六边形的特点求出阴影部分的面积和空白部分的面积,再根据概率公式即可得出答案.
解答 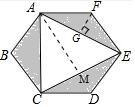 解:设正六边形的边长a,则FG=$\frac{a}{2}$,
解:设正六边形的边长a,则FG=$\frac{a}{2}$,
∵AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\frac{\sqrt{3}}{2}$a,
∴AE=$\sqrt{3}$a,
∴阴影部分的面积是:$\frac{1}{2}$AE•FG×3=$\frac{1}{2}$×$\sqrt{3}$a×$\frac{1}{2}$a×3=$\frac{3}{4}$$\sqrt{3}$a2,
空白部分的面积是:$\frac{1}{2}$CE•AM=$\frac{1}{2}$×$\sqrt{3}$a×$\frac{3}{2}$a=$\frac{3}{4}$$\sqrt{3}$a2,
∴小鸟在花圃上的概率为$\frac{1}{2}$;
故答案为:$\frac{1}{2}$.
点评 此题主要考查了几何概率问题,用到的知识点为:概率=相应的面积与总面积之比.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 500(1+x)=720 | B. | 500(1+x)2=720 | ||
| C. | 500(1+x)+500(1+x)2=720 | D. | 500x2=720 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com