
【题目】如图,在四边形 ![]() 中,
中, ![]() ,对角线
,对角线 ![]() 平分
平分 ![]() .
.
(1)求证: ![]() .
.
(2)若 ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)解:如图,

过 ![]() 点作
点作 ![]() ,
, ![]() ,
,
∵ ![]() 是
是 ![]() 的角平分线,
的角平分线,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]()
![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]() .
.
(2)解:∵ ![]() 且
且 ![]() 和
和 ![]() 为直角三角形,
为直角三角形,
∴设 ![]() ,
,
则 ![]() ,
, ![]() ,
,
而又∵ ![]() ≌
≌ ![]() ,
, ![]() ≌
≌ ![]() ,
,
∴ ![]() ,
,
即 ![]() ,解得
,解得 ![]() ,
,
∴ ![]() ,
,
则 ![]() 的长为
的长为 ![]()
【解析】(1)抓住已知条件AC平分 ∠B AD, 过C点作CE⊥AB , CF⊥AD,可证得CE=CF,再根据BC=CD,就可证明△CFD ≌ △CEB,得出∠D=∠EBC,然后根据∠EBC+∠B=180° ,即可证得结论。
(3)根据已知条件易证△BEC 和 △FDC 为等腰直角三角形,设它们的直角边长为x,就可表示出AE、AF的长,再根据全等三角形的性质证得AE=AF,建立关于x的方程,求出x的值,然后根据勾股定理,在Rt△ACF中就可求出AC的长。
【考点精析】通过灵活运用角平分线的性质定理和勾股定理的概念,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图所示,![]() 城市在
城市在![]() 城市正东方向,现计划在
城市正东方向,现计划在![]() 两城市间修建一条高速铁路(即线段
两城市间修建一条高速铁路(即线段![]() ),经测量,森林保护区的中心
),经测量,森林保护区的中心![]() 在城市
在城市![]() 的北偏东
的北偏东![]() 方向上,在线段
方向上,在线段![]() 上距
上距![]() 城市
城市![]() 的
的![]() 处测得
处测得![]() 在北偏东
在北偏东![]() 方向上,已知森林保护区是以点
方向上,已知森林保护区是以点![]() 为圆心,
为圆心,![]() 为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?
(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使(x2+px+8)(x2﹣3x+q)乘积中不含x2与x3项的p、q的值是( )
A.p=0,q=0
B.p=3,q=1
C.p=﹣3,q=﹣9
D.p=﹣3,q=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中放有若干个球,其中有6个白球,其余是红球,这些球除颜色外完全相同.每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则红球的个数约是( )
A.2B.12C.18D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 的一边
的一边 ![]() 为平面镜,
为平面镜, ![]() ,在
,在 ![]() 上有一点
上有一点 ![]() ,从
,从 ![]() 点射出一束光线经
点射出一束光线经 ![]() 上一点
上一点 ![]() 反射,反射光线
反射,反射光线 ![]() 恰好与
恰好与 ![]() 平行,则
平行,则 ![]() 的度数是( )
的度数是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A,B分别为x轴、y轴正半轴上两动点,∠BAO的平分线与∠OBA的外角平分线所在直线交于点C,则∠C的度数随A,B运动的变化情况正确的是( )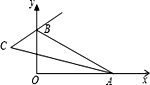
A.点B不动,在点A向右运动的过程中,∠C的度数逐渐减小
B.点A不动,在点B向上运动的过程中,∠C的度数逐渐减小
C.在点A向左运动,点B向下运动的过程中,∠C的度数逐渐增大
D.在点A,B运动的过程中,∠C的度数不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)
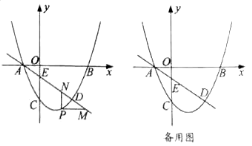
如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]()
![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() ,
,![]() 两点.
两点.![]() 为抛物线上一动点(不与
为抛物线上一动点(不与![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方时,过点
下方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() .求
.求![]() 的最大值;
的最大值;
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com