
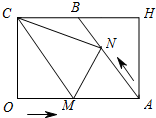
 ��ͼ���ھ���OAHC�У�OC=4��OA=6��BΪCH�е㣬����AB������M�ӵ�O������OA�����A�˶�������N�ӵ�A������AB�����B�˶�����������ͬʱ�������ٶȶ���ÿ��1����λ���ȣ�����CM��CN��MN�����˶�ʱ��Ϊt���룩��0��t��5��������������⣺
��ͼ���ھ���OAHC�У�OC=4��OA=6��BΪCH�е㣬����AB������M�ӵ�O������OA�����A�˶�������N�ӵ�A������AB�����B�˶�����������ͬʱ�������ٶȶ���ÿ��1����λ���ȣ�����CM��CN��MN�����˶�ʱ��Ϊt���룩��0��t��5��������������⣺���� ��1������A��MN�Ĵ�ֱƽ������ʱ����AM=AN���г����̼������t��ֵ��
��2������N��OA�Ĵ��ߣ���OA�ڵ�F����CH�ڵ�E������AM=6-t��AN=t���������þ��ε����ʺ����������ε����ʿ����EN=$\frac{4}{5}$��5-t����Ȼ��ֱ��������OABC����OMC����NCB�͡�AMN������������S��t�Ĺ�ϵ��
��3������2���еĹ�ϵʽ�����䷽�����ö��κ��������ʼ������S����Сֵ
��4����CMN��ֱ��������ʱ�������������һ�ǡ�CMN=90�㣬���ǡ�MNC=90�㣬���ǡ�MCN=90�㣬Ȼ����з����������t��ֵ��
��� �⣺��1������A��MN�Ĵ�ֱƽ������ʱ��
��ʱ��AM=AN��
��OM=t��
��AM=6-t��
��AN=t
��6-t=t��
��t=3��
��2������N��OA�Ĵ��ߣ���OA�ڵ�F����CH�ڵ�E����ͼ1��
��B����CH���е㣬
��BH=$\frac{1}{2}$CH=3��
��AH=OC=4��
���ɹ��ɶ�������AB=5��
��AN=t��
��BN=5-t��
��NE��AH��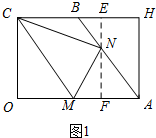
���BEN�ס�BHA��
��$\frac{BN}{AB}=\frac{EN}{AH}$��
��$\frac{5-t}{5}=\frac{EN}{4}$��
��EN=$\frac{4}{5}$��5-t����
��FN=4-EN=$\frac{4}{5}$t��
������OABC�����Ϊ��$\frac{1}{2}$��BC+OA��•OC=18��
��OMC�����Ϊ��$\frac{1}{2}$OM•OC=2t��
��NCB�����Ϊ��$\frac{1}{2}$BC•EN=$\frac{6}{5}$��5-t����
��AMN�����Ϊ��$\frac{1}{2}$AM•FN=$\frac{2}{5}$t��6-t����
��S=18-2t-$\frac{6}{5}$��5-t��-$\frac{2}{5}$t��6-t��
=$\frac{2}{5}$t2-$\frac{16}{5}$+12��
��3���ɣ�2����֪��S=$\frac{2}{5}$t2-$\frac{16}{5}$+12=$\frac{2}{5}$��t-4��2+$\frac{28}{5}$��
��0��t��5��
�൱t=4ʱ��S�����ֵΪ$\frac{28}{5}$��
��4������CMN=90�㣬
�ɣ�2����֪��FN=$\frac{4}{5}$t��
�ɹ��ɶ�������AF=$\frac{3}{5}$t��
��MF=AM-AF=6-t-$\frac{3}{5}$t=6-$\frac{8}{5}$t��
�ߡ�OCM+��CMO=90�㣬
��CMO+��FMN=90�㣬
���OCM=��FMN��
�ߡ�O=��NFM=90�㣬
���COM�ס�MFN��
��$\frac{OC}{MF}=\frac{OM}{FN}$��
��$\frac{4}{6-\frac{8}{5}t}=\frac{t}{\frac{4}{5}t}$��
��t=$\frac{7}{4}$��
����MNC=90�㣬
�ɣ�2����֪��FN=$\frac{4}{5}$t��
��EN=$\frac{4}{5}$��5-t����
��MF=6-$\frac{8}{5}$t��
��CE=OF=OM+MF=6-$\frac{3}{5}$t��
�ߡ�MNF+��CNE=90�㣬
��ECN+��CNE=90�㣬
���MNF=��ECN��
�ߡ�CEN=��NFM=90�㣬
���CEN�ס�NFM��
��$\frac{CE}{FN}=\frac{EN}{MF}$��
��$\frac{6-\frac{3}{5}t}{\frac{4}{5}t}=\frac{\frac{4}{5}��5-t��}{6-\frac{8}{5}t}$��
��t=$\frac{41��\sqrt{241}}{8}$��
��0��t��5��
��t=$\frac{41-\sqrt{241}}{8}$��
����NCM=90�㣬
������֪������������ڣ�
������������CMNΪֱ��������ʱ��t=$\frac{7}{4}$��$\frac{41-\sqrt{241}}{8}$��
���� ������Ҫ���������������ε��ж������ʡ����κ�������ֵ�����ɶ�����֪ʶ���õ��˸�����䷽������Ҫ����ѧ��������һ�����ۺ��ԣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x2-6x+1=0 | B�� | 3x2-x-5=0 | C�� | x2+x=0 | D�� | x2-4x+4=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 36��103 | B�� | 0.36��106 | C�� | 0.36��104 | D�� | 3.6��104 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����C��E��D���߶�AB�ϣ���AB=3AC��AB=4BD��AE=CD�����߶�CE��AB����֮��Ĺ�ϵ�ǣ�������
��ͼ����C��E��D���߶�AB�ϣ���AB=3AC��AB=4BD��AE=CD�����߶�CE��AB����֮��Ĺ�ϵ�ǣ�������| A�� | AB=12CE | B�� | AB=11CE | C�� | AB=10CE | D�� | AB=9CE |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com