如图等边三角形ABC内接于圆.点P是圆上任意一点.则∠APB=60°或120°．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

14．

如图等边三角形ABC内接于圆，点P是圆上任意一点（P不与A、B、C重合），则∠APB=60°或120°．

分析根据题意作出辅助线，再由圆周角定理即可得出结论．

解答解：如图，∵△ABC是等边三角形，
∴∠C=60°，
∴∠P=180°-60°=120°；∠P′=∠C=60°．
故答案为：60°或120°．

点评本题考查的是三角形的外接圆与外心，根据题意作出辅助线，构造出圆周角是解答此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

4．若中学生体质健康综合评定成绩为x分，满分为100分．规定：85≤x≤100为A级，75≤x＜85为B级，60≤x＜75为C级，x＜60为D级．现随机抽取某中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图．

请根据图中的信息，解答下列问题：
（1）在这次调查中，一共抽取了50名学生；a=24%；C级对应的圆心角为72度．
（2）补全条形统计图；
（3）若该校共有2000名学生，请你估计该校D级学生有多少名？

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

5．下表是四个城市今年二月份某一天的平均气温，其中平均气温最低的城市是（　　）

城市	吐鲁番	乌鲁木齐	喀什	阿勒泰
气温（℃）	-8	-16	-5	-25

A．

吐鲁番

B．

乌鲁木齐

C．

喀什

D．

阿勒泰

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．

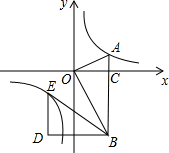如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（$\sqrt{3}$，1）在反比例函数y=$\frac{k}{x}$的图象上．
（1）求反比例函数y=$\frac{k}{x}$的表达式；
（2）在x轴的负半轴上存在一点P，使得S_△AOP=$\frac{1}{2}$S_△AOB，求点P的坐标；
（3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

9．若买2支圆珠笔、1本笔记本需14元；买1支圆珠笔，2本笔记本需16元，则买5支圆珠笔、5本笔记本需50元．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．如图1，在平面直角坐标系xOy中，抛物线y=x²+bx+c与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（4，0），将直线y=kx沿y轴向上平移4个单位长度后恰好经过B，C两点．

（1）求直线BC及抛物线的解析式；
（2）将直线BC沿y轴向上平移5个单位长度后与抛物线交于D，E两点，若点P是抛物线位于直线BC下方的一个动点，连接PD，交直线BC于点Q，连接PE和PQ．设△PEQ的面积为S，当S取得最大值时，求出此时点P的坐标及S的最大值；
（3）如图2，记（2）问中直线DE与y轴交于M点，现有一点N从M点出发，先沿y轴到达K点，再沿KB到达B点，已知N点在y轴上运动的速度是每秒2个单位长度，它在直线KB上运动速度是1个单位长度．现要使N点按照上述要求到达B点所用的时间最短，请简述确定K点位置的过程，求出点K的坐标，不要求证明．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

6．

如图，G为△ABC的重心，DE过点G，且DE∥BC，交AB、AC，分别于D、E两点，则△ADE与△ABC的面积之比为$\frac{4}{9}$．