
如图,在△ABC中,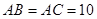 cm,
cm,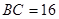 cm,
cm,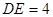 cm,动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达C时运动停止,过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为
cm,动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达C时运动停止,过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为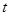 秒(
秒(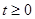 )
)
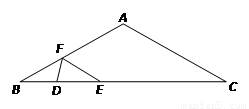
(1)直接写出用含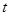 的代数式表示线段BE、EF的长;
的代数式表示线段BE、EF的长;
(2)在这个动动过程中,△DEF能否为等腰三角形?若能,请求出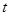 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(3)设M、N分别是DF、EF的中点,求整个运动过程中,MN所扫过的面积。
(1)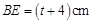 ,
,
 .(2)
.(2)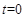 、
、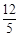 或
或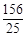 (3)
(3)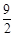
【解析】解:(1)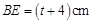 ,···················· 1分
,···················· 1分
 .···························· 4分
.···························· 4分
(2)分三种情况讨论:
①当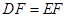 时,
时,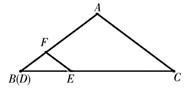
有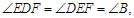
∴点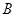 与点
与点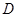 重合,
重合,
∴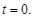 ············ 5分
············ 5分
②当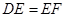 时,
时, 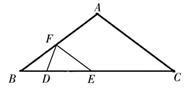
∴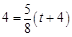 ,
,
解得: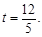 ········· 7分
········· 7分
③当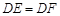 时,
时, 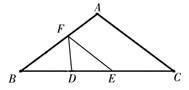
有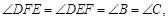
∴△DEF∽△ABC.
∴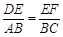 , 即
, 即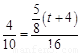 ,
,
解得: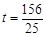 . ········ 9分
. ········ 9分
综上所述,当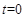 、
、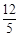 或
或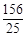 秒时,△
秒时,△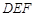 为等腰三角形.
为等腰三角形.
(3)设P是AC的中点,连接BP,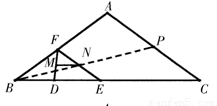
∵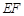 ∥
∥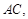
∴△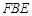 ∽△
∽△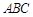 .
.
∴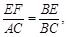 ∴
∴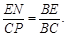
又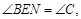 ∴△
∴△ ∽△
∽△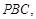
∴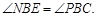 ··························· 10分
··························· 10分
∴点 沿直线BP运动,MN也随之平移.
沿直线BP运动,MN也随之平移.
如图,设MN从ST位置运动到PQ位置,则四边形PQST是平行四边形. 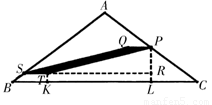
∵ 、
、 分别是
分别是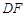 、
、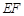 的中点,∴
的中点,∴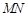 ∥DE,且ST=MN=
∥DE,且ST=MN=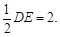
分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,
当t=0时,EF=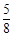 (0+4)=
(0+4)=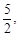 TK=
TK=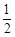 EF·
EF·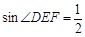 ·
·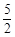 ·
·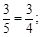
当t=12时,EF=AC=10,PL=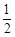 AC·
AC·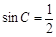 ·10·
·10·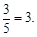
∴PR=PL-RL=PL-TK=3-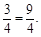
∴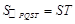 ·PR=2×
·PR=2×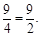
∴整个运动过程中,MN所扫过的面积为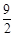 cm2. 13分
cm2. 13分
(1)由题意得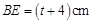 ,利用相似比求出EF的长
,利用相似比求出EF的长
(2)分三种情况讨论:①当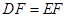 时,②当
时,②当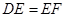 时, ③当
时, ③当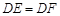 时
时
(3)设P是AC的中点,连接BP,通过相似证得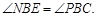 ,
, 、
、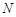 分别是
分别是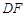 、
、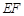 的中点,求得ST=2 ,分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,利用三角函数求得PL、TK的值,得出PR的值,从而得出结论
的中点,求得ST=2 ,分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,利用三角函数求得PL、TK的值,得出PR的值,从而得出结论


科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com