
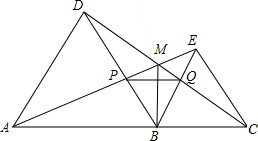
 如图,点A、B、C在同一直线上,△ABD、△BCE均为正三角形,连接AE、CD交于点M,AE交BD于点P,CD交BE于点Q,连接PQ、BM,则下列说法:
如图,点A、B、C在同一直线上,△ABD、△BCE均为正三角形,连接AE、CD交于点M,AE交BD于点P,CD交BE于点Q,连接PQ、BM,则下列说法:分析 ①由等边三角形的性质得出AB=DB,∠ABD=∠CBE=60°,BE=BC,得出∠ABE=∠DBC,由SAS即可证出△ABE≌△DBC;
②由△ABE≌△DBC,即可得到DC=AE;
③由ASA证明△ABP≌△DBQ,得出对应边相等BP=BQ,即可得出△BPQ为等边三角形;
④推出△BPQ是等边三角形,得到∠PBQ=60°,根据平行线的性质即可得到PQ∥AC.
解答 解:∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠PBQ=60°,
在△ABE和△DBC中,
$\left\{\begin{array}{l}{AB=DB}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△DBC(SAS),
∴①正确;
∵△ABE≌△DBC,
∴AE=DC,
∴②正确;
在△ABP和△DBQ中,
$\left\{\begin{array}{l}{∠BAP=∠BDQ}\\{AB=DB}\\{∠ABP=∠DBQ=60°}\end{array}\right.$,
∴△ABP≌△DBQ(ASA),
∴BP=BQ,
∴△BPQ为等边三角形,
∴③正确;
∵BP=BQ,∠PBQ=60°,
∴△BPQ是等边三角形,
∴∠PQB=60°,
∴∠PQB=∠QBC,
∴PQ∥AC,
故④正确.
故答案为①②③④.
点评 此题考查了等边三角形的判定与性质与全等三角形的判定与性质,平行线的判定和性质,此题图形比较复杂,解题的关键是仔细识图,找准全等的三角形.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
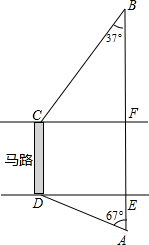 如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.
如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
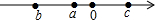 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )| A. | -3a | B. | -a+2b-2c | C. | 2b | D. | a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 2 | 4 | 3 | 1 |
| A. | 16,14 | B. | 14,14 | C. | 14,15 | D. | 15,14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com