练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等式的性质

    (1)等式两边加(或减)________，结果仍相等．

    如果a＝b，那么a±c＝________．

    (2)等式两边乘同一个数，或除以________，结果仍相等．

    如果a＝b，那么ac＝________；如果a＝b(c≠0)，那么＝________．

    答案：相同的一个数或整式；b±c;一个不等于0的数；bc;b\c.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    29、如图，已知点D、E为△ABC的边BC上两点．AD=AE，BD=CE，为了判断∠B与∠C的大小关系，请你填空完成下面的推理过程，并在空白括号内注明推理的依据．
    解：过点A作AH⊥BC，垂足为H．
    ∵在△ADE中，AD=AE（已知）
    AH⊥BC（所作）
    ∴DH=EH（等腰三角形底边上的高也是底边上的中线）
    又∵BD=CE（已知）
    ∴BD+DH=CE+EH（等式的性质）
    即：BH=
    CH

    又∵
    AH⊥BC
    （所作）
    ∴AH为线段
    BC
    的垂直平分线
    ∴AB=AC（线段垂直平分线上的点到线段两个端点的距离相等）
    ∴
    ∠B=∠C
    （等边对等角）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，点B、E、C、F在同一直线上，且AB=DE，AC=DF，BE=CF，请将下面说明∠A=∠D的过程和理由补充完整．
    解：∵BE=CF （
    已知
    已知
    ），
    ∴BE+EC=CF+EC （
    等式的性质
    等式的性质
    ） 即BC=EF，
    在△ABC和△DEF中，
    AB=
    DE
    DE

    AC
    AC
    =DF
    BC=EF，
    ∴△ABC≌△DEF
    SSS
    SSS
    ，
    ∴∠A=∠D（
    全等三角形的对应角相等
    全等三角形的对应角相等
     ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （阅读理解题）如图所示，CE⊥AB于点E，BD⊥AC于点D，BD，CE交于点O，且AO平分∠BAC．
    （1）图中有多少对全等三角形？请一一列举出来（不必说明理由）；
    （2）小明说：欲证BE=CD，可先证明△AOE≌△AOD得到AE=AD，再证明△ADB≌△AEC得到AB=AC，然后利用等式的性质得到BE=CD，请问他的说法正确吗？如果正确，请按照他的说法写出推导过程，如果不正确，请说明理由；
    （3）要得到BE=CD，你还有其他思路吗？若有，请写出推理过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先填写完成第（1）小题中的空缺部分（数学表达式或理由），再按要求解答第（2）小题．
    如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．
    （1）求证：AB=DC；
    （2）请你连接AE、DF．问AE和DF相等吗？为什么？
    证明：
    （1）∵BE=CF（已知），
    ∴BE+EF=CF+EF（
    等式的性质
    等式的性质
    ），
    即BF=CE．
    在△ABF和△DCE中，
    ∠A=(    )(   )
    (   )(    )
    (     )(    )

    ∴△ABF≌△DCE
    （AAS）
    （AAS）
    ，
    ∴AB=DC
    （全等三角形的对应边相等）
    （全等三角形的对应边相等）
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

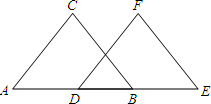    看图填空：
    已知：如图，BC∥EF，AD=BE，BC=EF，试说明 AC=DF
    解：∵AD=BE
    ∴AD+DB=BE+
    DB
    DB
    （等式的性质）
    即：AB=
    DE
    DE

    ∵BC∥EF
    ∴∠ABC=∠
    DEF
    DEF
    （
    两直线平行，同位角相等
    两直线平行，同位角相等
    ）
    在△ABC和△DEF中
    BC=EF (已知)
    (     )(已证)
    AB=DE (已证)

    ∴△ABC≌△DEF（
    SAS
    SAS
    ）
    ∴AC=DF （
    全等三角形的对应边相等
    全等三角形的对应边相等
    ）．

    查看答案和解析>>

    同步练习册答案