
分析 (1)如果每件商品的售价每上涨1元,则每个月少卖2件,可得销售量为100-2(x-60),销售量乘以利润即可得到等式[100-2(x-60)](x-40)=2250,解答即可;
(2)将(1)中的2250换成y即可解答.
解答 解:(1)[100-2(x-60)](x-40)=2250,
解得:x1=65,x2=85.
(2)由题意:y=[100-2(x-60)](x-40)=-2x2+300x-8800;
y=-2(x-75)2+2450,当x=75时,y有最大值为2450元.
点评 本题考查了一元二次方程的应用和二次函数的应用,最大销售利润的问题常利用函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
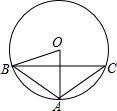 如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=4,则弦BC的长为( )
如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=4,则弦BC的长为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com