练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】 如图，梯形ABCD中，AB//CD，且AB=2CD，E，F分别是AB，BC的中点．

    EF与BD相交于点M．

    （1）求证：△EDM∽△FBM；

    （2）若DB=9，求BM．

    【答案】（1）证明见解析（2）3

    【解析】试题分析：(1)、根据中点的性质得出AB=2CD，则BE=CD，集合AB∥CD得出四边形BEDC是平行四边形，从而得到三角形相似；(2)、根据三角形相似和DM=2BM，BD=DM+BM=9得出BM的长

    试题解析：(1)、证明：∵点E、F分别是AB、BC的中点且AB=2CD，

    ∴BE=CD．∵AB∥CD，∴四边形BEDC是平行四边形．∴DE∥BF ∴△EDM∽△FBM

    (2)、∵△EDM∽△FBM， ∴∴DM=2BM．∵BD=DM+BM=9， ∴BM=3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列说法错误的是（　　）
    A.若两角互余，则两角均为锐角
    B.若两角相等，则它们的补角也相等
    C.互为余角的补角相等
    D.两个钝角不能互补

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程组：

    （1）

    （2） ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司欲招聘一名工作人员，对甲、乙两位应聘者进行面试和笔试，他们的成绩（百分制）如表所示．

    应聘者

    面试

    笔试

    甲

    87

    90

    乙

    91

    82

    若公司分别赋予面试成绩和笔试成绩6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在大小为4×4的正方形网格中，是相似三角形的是（　　）

    A. ①和② B. ②和③ C. ①和③ D. ②和④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，等腰△ABC中，AC=BC＝, ∠ACB=45，AO是BC边上的高，D为线段AO上一动点，以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45，连结BE.

    (1) 求证：△ACD≌△BCE；

    (2) 如图2，在图1的基础上，延长BE至Q, P为BQ上一点，连结CP、CQ,若CP＝CQ＝5,求PQ的长.

    (3) 连接OE，直接写出线段OE的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图所示的网格中，线段AB和直线l如图所示：

    （1）借助图中的网格，在图1中作锐角△ABC，满足以下要求：①C为格点（网格线交点）；②AB=AC．

    （2）在（1）的基础上，请只用直尺（不含刻度）在图（1）中找一点P，使得P到AB、AC的距离相等，且PA＝PB．（友情提醒：请别忘了标注字母！）

    （3）在图2中的直线l上找一点Q，使得△QAB的周长最小，并求出周长的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明想知道旗杆的高度，他发现旗杆顶端的绳子垂到地面还多出1米，他把绳子的下端往外拉开5米后，发现下端刚好接触地面，求旗杆的高度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

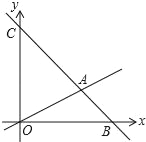
    【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．

    （1）求直线AB的解析式．

    （2）求△OAC的面积．

    （3）是否存在点M，使△OMC的面积是△OAC的面积的？若存在求出此时点M的坐标；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案