练习册

  • 练习册
  • 试题
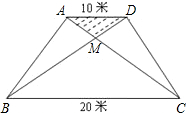    精英家教网 > 初中数学 > 题目详情

    如图，梯形上、下底分别为a，b，高线长恰好等于圆的直径2r，则图中阴影部分的面积是


    1. A.
      （a+b）r-πr2
    2. B.
      abr-πr2
    3. C.
      2（a+b）r-πr2
    4. D.
      2abr-πr2
    A
    分析：本题的等量关系为：图中阴影部分的面积=梯形面积-圆的面积．根据等量关系直接求出结果．
    解答：依题意得，
    ×（a+b）×2r-π×（）2=（a+b）r-πr2．
    故选A．
    点评：解决问题的关键是读懂题意，找到所求的量的等量关系．需注意梯形面积、圆的面积公式的运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    某社区拟筹资金2000元，计划在一块上、下底分别是10米、20米的梯形空地上种植花木（如图所示），他们想在△AMD和△BMC地带种植单价为10元/米2的太阳花，当△AMD地精英家教网带种满花后，已经花了500元，请你预算一下，若继续在△BMC地带种植同样的太阳花，资金是否够用？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•黄石）如图1，点C将线段AB分成两部分，如果
    AC
    AB
    =
    BC
    AC
    ，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果
    S1
    S
    =
    S2
    S1
    ，那么称直线l为该图形的黄金分割线．
    （1）如图2，在△ABC中，∠A=36°，AB=AC，∠C的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
    （2）若△ABC在（1）的条件下，如图3，请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
    （3）如图4，在直角梯形ABCD中，∠D=∠C=90°，对角线AC、BD交于点F，延长AB、DC交于点E，连接EF交梯形上、下底于G、H两点，请问直线GH是不是直角梯形ABCD的黄金分割线，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：013

    如图，梯形上、下两底长分别为3和9，两腰长分别为4、6，平行于底的直线分梯形周长相等的两部分，那么这条直线将两腰分成两条线段比是（　）

    A．4∶1　　　　　　　　　　　　　　　　　　　　   B．3∶1

    C．4∶3　　　　　　　　　　　　　　　　　　　　   D．3∶2

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（湖北黄石卷）数学（带解析） 题型：解答题

    如图1，点C将线段AB分成两部分，如果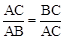，那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果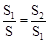，那么称直线l为该图形的黄金分割线.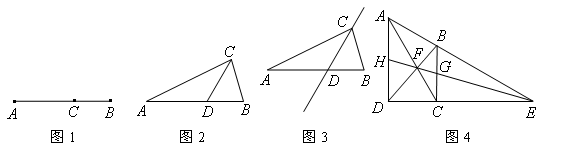

    （1）如图2，在△ABC中，∠A=360°，AB=AC，∠C的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
    （2）若△ABC在（1）的条件下，如图（3），请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
    （3）如图4，在直角梯形ABCD中，∠D=∠C=900，对角线AC、BD交于点F，延长AB、DC交于点E，连接EF交梯形上、下底于G、H两点，请问直线GH是不是直角梯形ABCD的黄金分割线，并证明你的结论.

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（湖北黄石卷）数学（解析版） 题型：解答题

    如图1，点C将线段AB分成两部分，如果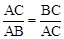，那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果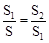，那么称直线l为该图形的黄金分割线.

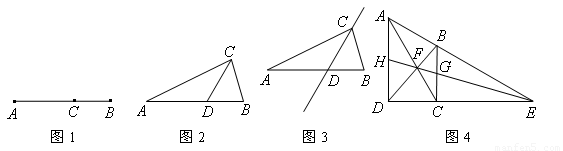
    （1）如图2，在△ABC中，∠A=360°，AB=AC，∠C的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；

    （2）若△ABC在（1）的条件下，如图（3），请问直线CD是不是△ABC的黄金分割线，并证明你的结论；

    （3）如图4，在直角梯形ABCD中，∠D=∠C=900，对角线AC、BD交于点F，延长AB、DC交于点E，连接EF交梯形上、下底于G、H两点，请问直线GH是不是直角梯形ABCD的黄金分割线，并证明你的结论.

     

    查看答案和解析>>

    同步练习册答案