
【题目】用适当的方法计算:
(1)0.36+(-7.4)+0.5+(-0.6)+0.14;
(2)(-2.125)+![]() +(-3.2);
+(-3.2);
(3)![]() .
.
(4)|-0.75|+(-3)-(-0.25)+![]() .
.
(5)![]()
【答案】(1)-7;(2)3;(3)![]() ;(4)-1;(5)
;(4)-1;(5)![]()
【解析】
利用有理数混合运算法则以及简便算法解答即可,利用加法交换律解(1)(2)(3)(4)更简便.
(1)0.36+(-7.4)+0.5+(-0.6)+0.14;
解:原式=(0.36+0.14)+[(-7.4)+(-0.6)]+0.5
=0.5+(-8)+0.5
=-7.
(2)(-2.125)+(+3![]() )+(+5
)+(+5![]() )+(-3.2);
)+(-3.2);
解:原式=[(-2.125)+(+5![]() )]+[(+3
)]+[(+3![]() )+(-3.2)]
)+(-3.2)]
=3.
(3)(-2![]() )+(+3
)+(+3![]() )+(-3
)+(-3![]() )+(+2
)+(+2![]() )+(-1
)+(-1![]() )+(+1
)+(+1![]() ).
).
解:原式=[(-2![]() )+(-3
)+(-3![]() )]+[(+3
)]+[(+3![]() )+(+2
)+(+2![]() )]+[(-1
)]+[(-1![]() )+(+1
)+(+1![]() )]
)]
=(-6)+6+(-![]() )
)
=-![]() .
.
(4)|-0.75|+(-3)-(-0.25)+|-![]() |+
|+![]() .
.
解:原式=0.75-3+0.25+![]() +
+![]()
=(0.75+0.25)+(![]() +
+![]() )-3
)-3
=1+1-3
=-1.
(5)(-81)÷(+3![]() )×(-
)×(-![]() )÷(-1
)÷(-1![]() );
);
解:原式=-81÷![]() ×
×![]() ÷
÷![]()
=-81×![]() ×
×![]() ×
×![]()
=-10![]() .
.


科目:初中数学 来源: 题型:
【题目】光华中学库存若干套桌椅,准备修理后支援贫困山区学校.现有甲、乙两修理组,甲修理组单独完成任务需要12天,乙修理组单独完成任务需要24天.
(1)若由甲、乙两修理组同时修理,需多少天可以修好这些套桌椅?
(2)若甲、乙两修理组合作3天后,甲修理组因新任务离开,乙修理组继续工作.甲完 成新任务后,回库与乙又合作3天,恰好完成任务.问:甲修理组离开几天?
(3)学校需要每天支付甲修理组、乙修理组修理费分别为80元,120元.任务完成后, 两修理组收到的总费用为1920元,求甲修理组修理了几天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验室:
![]()
我们知道,在数轴上,|a|表示数a的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上的两个点A、B,分别表示有理数a、b,那么A、B两点之间的距离AB=|a-b|.利用此结论,回答以下问题:
(1)数轴上表示1和5的两点之间的距离是______,数轴上表示1和-5的两点之间的距离是______.(1+1分,注意写出最后结果)
(2)式子|x+2|可以看做数轴上表示x和______的两点之间的距离.
(3)式子|x+2|+|x-3|的最小值是______.
(4)当|x+2|+|x-3|取得最小值时,数x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:对于排好顺序的三个数:![]() 称为数列
称为数列![]() .将这个数列如下式进行计算:
.将这个数列如下式进行计算: ![]() ,
,![]() ,
,![]() ,所得的三个新数中,最大的那个数称为数列
,所得的三个新数中,最大的那个数称为数列![]() 的“关联数值”.
的“关联数值”.
例如:对于数列![]() 因为
因为![]()
![]()
![]() 所以数列
所以数列![]() 的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列
的“关联数值”为6.进一步发现:当改变这三个数的顺序时,所得的数列都可以按照上述方法求出“关联数值”,如:数列![]() 的 “关联数值”为0;数列
的 “关联数值”为0;数列![]() 的“关联数值”为3...而对于“
的“关联数值”为3...而对于“![]() ”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.
”这三个数,按照不同的排列顺序得到的不同数列中,“关联数值"的最大值为6.
(1)数列![]() 的“关联数值”为_______;
的“关联数值”为_______;
(2)将“![]() ”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______
”这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值是_______, 取得“关联数值”的最大值的数列是______
(3)将“![]() ”
”![]() 这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求
这三个数按照不同的顺序排列,可得到若干个不同的数列,这些数列的“关联数值”的最大值为10,求![]() 的值,并写出取得“关联数值”最大值的数列.
的值,并写出取得“关联数值”最大值的数列.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,画直线
,画直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,有下列结论:
,有下列结论:
①![]() ; ②
; ②![]() 的大小随着
的大小随着![]() 的变化而变化;
的变化而变化;
③当![]() 时,四边形
时,四边形![]() 为菱形; ④
为菱形; ④![]() 面积的最大值为
面积的最大值为![]() ;
;

其中正确的是_____________.(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
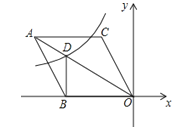
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖南省益阳市)在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线![]() 的图象上有一对“互换点”A、B,其中点A在反比例函数
的图象上有一对“互换点”A、B,其中点A在反比例函数![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P(![]() ,
,![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
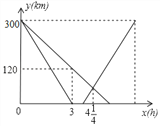
【题目】某客运公司的特快巴士与普通巴士同时从甲地出发,以各自的速度匀速向乙地行驶,普通巴士到达乙地后停止,特快巴士到达乙地停留45分钟后,按原路以另一速度匀速返回甲地,已知两辆巴士分别距乙地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示.求普通巴士到达乙地时,特快巴士与甲地之间的距离为_____千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com