
【题目】解下列方程:
(1)![]() x22x7=0
x22x7=0
(2)![]() 2(x1)2=1x
2(x1)2=1x
【答案】
(1)解:∵ x22x=7,
∴x22x+1=7+1,
即(x1)2=8,
∴x1=2![]() 或x1=-2
或x1=-2![]() ,
,
即x1=1+2![]() ,x2=12
,x2=12![]() .
.
(2)解:∵ 2(x1)2=(x1),
∴2(x1)2+(x1)=0,
∴(x1)[2(x1)+1]=0,
∴x1=0或2(x1)+1=0,
∴x1=1,x2=![]() .
.
【解析】(1)根据配方法和直接开平方法即可解方程.
(2)根据因式分解——提公因式法即可解方程.
【考点精析】利用直接开平方法和配方法对题目进行判断即可得到答案,需要熟知方程没有一次项,直接开方最理想.如果缺少常数项,因式分解没商量.b、c相等都为零,等根是零不要忘.b、c同时不为零,因式分解或配方,也可直接套公式,因题而异择良方;左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
![]() 若
若![]() ,求线段MN的长;
,求线段MN的长;
![]() 若C为线段AB上任一点,满足
若C为线段AB上任一点,满足![]() ,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
![]() 若C在线段AB的延长线上,且满足
若C在线段AB的延长线上,且满足![]() cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
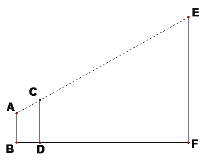
【题目】(1)在一次测量旗杆高度的活动中,某小组使用的方案如下:AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面。若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度。
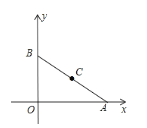
(2)如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6),点C是线段AB的中点。请问在x轴上是否存在一点P,使得以P、A、C为顶点的三角形与△AOB相似?若存在,求出P点坐标(写出计算的过程);若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是AC上一点,E是AB上一点,且∠AED=∠C.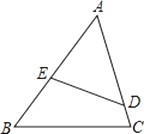
(1)求证:△AED∽△ACB;
(2)若AB=6,AD=4,AC=5,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com