
 四边形ABCD中,E、F分别是BD、AC中点,求证:三角形EFG面积等于四边形AEFD的面积.
四边形ABCD中,E、F分别是BD、AC中点,求证:三角形EFG面积等于四边形AEFD的面积. 分析 先利用三角形的一条中线将三角形分成面积相等的两个三角形,以及面积的和与差得出S△GFE=$\frac{1}{4}$S四边形ABCD①,再利用三角形的一条中线将三角形分成面积相等的两个三角形得出S四边形AEFD=$\frac{1}{4}$S四边形ABCD②,由①②即可得出结论.
解答 证明:如图,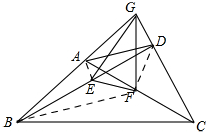
连接DF,FB,
∵点F是AC中点,
∴S△AFD=$\frac{1}{2}$S△ACD;
S△AFB=$\frac{1}{2}$S△ACB.
∵点E,F分别是BD,AC中点,
∴AF=FC;DE=EB;
∴S△GFE=(S△GFC+S△BFC)-S△FEB-S△GEB;
S△GFE=($\frac{1}{2}$S△GAC+$\frac{1}{2}$S△BAC)-$\frac{1}{2}$S△FDB-$\frac{1}{2}$S△GDB.
∴2S△GFE=S△GAB-S△FDB-S△GDB=S△ADF+S△AFB;
即2S△GFE=$\frac{1}{2}$S△ACD+$\frac{1}{2}$S△ACB=$\frac{1}{2}$S四边形ABCD.
∴S△GFE=$\frac{1}{4}$S四边形ABCD①
∵BE=DE,
∴S△DEF=$\frac{1}{2}$S△BDF,
S△ADE=$\frac{1}{2}$S△ABD,
∴S四边形AEFD=S△DEF+S△ADE=$\frac{1}{2}$S△BDF+$\frac{1}{2}$S△ABD=$\frac{1}{2}$(S△BDF+S△ABD)=$\frac{1}{2}$S四边形ABFD,
∵AF=CF,
∴S△ADF=$\frac{1}{2}$S△ACD,
S△ABF=$\frac{1}{2}$S△ABC,
∴S四边形ABFD=S△ACD+S△ABF=$\frac{1}{2}$S△ACD+$\frac{1}{2}$S△ABC=$\frac{1}{2}$(S△ABC+S△ACD)=$\frac{1}{2}$S四边形ABCD
∴S四边形AEFD=$\frac{1}{2}$S四边形ABFD=$\frac{1}{2}$×$\frac{1}{2}$S四边形ABCD=$\frac{1}{4}$S四边形ABCD②
由①②得,S△PFE=S四边形AEFD
即:三角形EFG面积等于四边形AEFD的面积.
点评 此题是面积及等积变换,主要考查了三角形的中线的性质,中点的意义,面积的和差,解本题的关键是三角形的一条中线分成的两个三角形的面积相等,难点是用三角形的中线和面积的和差得出S△GFE=$\frac{1}{4}$S四边形ABCD.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{22}{7}$和$\sqrt{7}$ | B. | $\sqrt{7}和\frac{π}{2}$ | C. | $\sqrt{7}和\sqrt{25}$ | D. | $\frac{22}{7}$和$\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为4,点G在BC边上,BG=3,连接AG,DE⊥AG于点E,BF⊥AG于点F.
如图,正方形ABCD的边长为4,点G在BC边上,BG=3,连接AG,DE⊥AG于点E,BF⊥AG于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1≤y2 | C. | y1>y2 | D. | y1≥y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ | B. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | C. | $\sqrt{(-3)^{2}}$=±3 | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com