
分析 (1)先通分,公分母为xy,再约分得-$\frac{2y}{x}$;
(2)先把括号内的进行通分,公分母为a+2,再把除法化成乘法,进行约分.
解答 解:(1)$\frac{x}{y}$-$\frac{y}{x}$-$\frac{{x}^{2}+{y}^{2}}{xy}$,
=$\frac{{x}^{2}-{y}^{2}-{x}^{2}-{y}^{2}}{xy}$,
=$\frac{-2{y}^{2}}{xy}$,
=-$\frac{2y}{x}$;
(2)(1-$\frac{1}{a+2}$)÷$\frac{{a}^{2}-1}{a+2}$,
=$\frac{a+2-1}{a+2}$•$\frac{a+2}{(a+1)(a-1)}$,
=$\frac{a+1}{(a+1)(a-1)}$,
=$\frac{1}{a-1}$.
点评 本题是分式的混合运算,分式的混合运算,一般按常规运算顺序,但有时也会根据题目的特点,运用乘法的运算律进行灵活运算;注意符号问题和化简结果:运算的结果要化成最简分式或整式.


科目:初中数学 来源: 题型:解答题
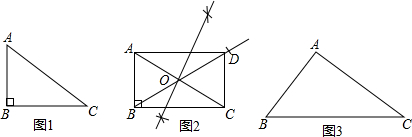
 如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF.
如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
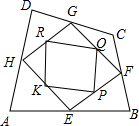 如图,铎山中心学校校园内有一块四边形空地ABCD,学校征集对这块空地种植的花草的设计中,选定如下方案:把这个四边形分成九块,种植三种不同的花草,其中E、F、G、H分别是AB、BC、CD、DA的中点,P、Q、R、K分别是EF、FG、GH、HE的中点,现要在四边形PQRK中种上红色的花,在△PFQ、△QGR、△RHK、△KEP中种上黄色的花,在△HAE、△EBF、△FCG、△GDH中种上紫色的花.已知种红、黄、紫三种花的单价分别为10元/m2、12元/m2、14元/m2,而种红花已用去了120元.请你用学过的数学知识计算出种满四边形ABCD这块空地的花共需要多少元?
如图,铎山中心学校校园内有一块四边形空地ABCD,学校征集对这块空地种植的花草的设计中,选定如下方案:把这个四边形分成九块,种植三种不同的花草,其中E、F、G、H分别是AB、BC、CD、DA的中点,P、Q、R、K分别是EF、FG、GH、HE的中点,现要在四边形PQRK中种上红色的花,在△PFQ、△QGR、△RHK、△KEP中种上黄色的花,在△HAE、△EBF、△FCG、△GDH中种上紫色的花.已知种红、黄、紫三种花的单价分别为10元/m2、12元/m2、14元/m2,而种红花已用去了120元.请你用学过的数学知识计算出种满四边形ABCD这块空地的花共需要多少元?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,公园内有一小湖,为了测量湖边B、C两点间的距离,小明设计如下方案,选取一个合适的A点,分别找到AB、AC的中点D、E,若测得DE的长为35米,则B、C两点间的距离为70米.
如图,公园内有一小湖,为了测量湖边B、C两点间的距离,小明设计如下方案,选取一个合适的A点,分别找到AB、AC的中点D、E,若测得DE的长为35米,则B、C两点间的距离为70米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com