
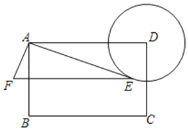
【题目】如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=![]() ,则点F与点C的最小距离为_____.
,则点F与点C的最小距离为_____.
【答案】3![]() ﹣1 .
﹣1 .
【解析】
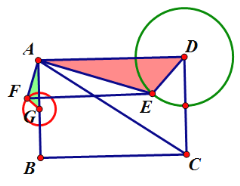
如图,取AB的中点G,连接FG,根据已知条件易证△AFG∽△EAD,根据相似三角形的性质求得FG=1;即可得点F在以点G为圆心,半径为1的圆上,所以当点F在线段GC上时,点F与点C的距离最小,由此即可求得点F与点C的最小距离.
如图,取AB的中点G,连接FG,
∵AB=4,AD=6,
∴AG=2,![]() ;
;
在Rt△AEF,∠EAF=90°,tan∠AEF=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠EAF=∠BAD=90°,
∴∠FAG=∠EAD,
∴△AFG∽△EAD,
∴![]() ,
,
∵DE=3,
∴FG=1;
∵点E为⊙D上一动点,
∴点F在以点G为圆心,半径为1的圆上,
∴当点F在线段GC上时,点F与点C的距离最小,
在Rt△GBC中,BC=6,GB=3,由勾股定理求得GC=3![]() ,
,
∴FC=3![]() ﹣1.
﹣1.
即点F与点C的最小距离为3![]() ﹣1.
﹣1.
故答案为:3![]() ﹣1.
﹣1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
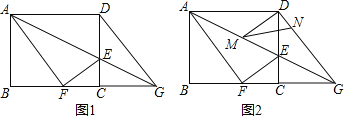
【题目】如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.
(1)求线段CE的长;
(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.
①写出y关于x的函数解析式,并求出y的最小值;
②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
节目 | 人数(名) | 百分比 |
最强大脑 |
|
|
朗读者 |
|
|
中国诗词大会 |
|
|
出彩中国人 |
|
|
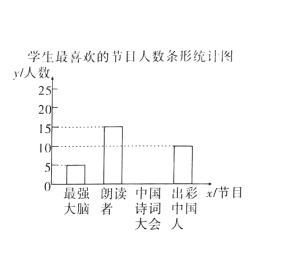
根据以上提供的信息.解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 补全上面的条形统计图;
补全上面的条形统计图;
![]() 名女同学.其余为男同学,现要从中随机抽取
名女同学.其余为男同学,现要从中随机抽取![]() 名同学代表学校参加市里组织的竞赛活动,请求出所抽取的
名同学代表学校参加市里组织的竞赛活动,请求出所抽取的![]() 名同学恰好是
名同学恰好是![]() 名男同学和
名男同学和![]() 名女同学的概率.
名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在正方形![]() 中,
中,![]() 是
是![]() 一点,
一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() ;
;
拓展:在图①中,若![]() 在
在![]() ,且
,且![]() ,则
,则![]() 成立吗?为什么?
成立吗?为什么?
运用:如图②在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,小李同学对该函数的图象与性质进行了探究,下面是小李同学探究的过程,补充完整:
,小李同学对该函数的图象与性质进行了探究,下面是小李同学探究的过程,补充完整:
(1)直接写出自变量x的取值范围:__________;
(2)下表是y与x的几组对应值:
x | … | -4 | -1 | 0 |
| 1 |
|
| 3 |
| 4 | 5 | n | … |
y | … |
| m |
| 0 | -1 | -4 | 8 | 5 | 4 |
| 3 |
| … |
则m= ,n= ;
(3)如图所示,在平面直角坐标系xoy中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;
(4)观察函数图象可知:该函数图象的对称中心的坐标是______;
(5)当![]() 时,关于x的方程
时,关于x的方程![]() 有实数解,直接写出k的取值范围_______.
有实数解,直接写出k的取值范围_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年1月份,为抗击新型冠状病毒,某药店计划购进一批甲、乙两种型号的口罩,已知一袋甲种口罩的进价与一袋乙种口罩的进价和为40元,用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同.
(1)求每袋甲种、乙种口罩的进价分别是多少元?
(2)该药店计划购进甲、乙两种口罩共480袋,其中甲种口罩的袋数少于乙种口罩袋数的![]() ,药店决定此次进货的总资金不超过10000元,求商场共有几种进货方案?
,药店决定此次进货的总资金不超过10000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
(1)求证:∠BME=∠MAB;
(2)求证:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求线段AM的长.
,求线段AM的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com