
分析 先求出该抛物线的对称轴,然后根据对称轴的位置即可求出a的取值范围.
解答 解:抛物线的对称轴为:x=$\frac{a}{3}$,
当$\frac{a}{3}$≤-$\frac{1}{3}$时,
即:a≤-1,
此时函数y在-$\frac{1}{3}$≤x≤$\frac{1}{3}$上,y随着x的增大而增大,
∴x=-$\frac{1}{3}$,y=a2-5>0,
∴a<-$\sqrt{5}$或a>$\sqrt{5}$
∴a<-$\sqrt{5}$
当-$\frac{1}{3}$<$\frac{a}{3}$<$\frac{1}{3}$时,
即:-1<a<1,
∴此时-$\frac{1}{3}$≤x≤$\frac{1}{3}$时,y>0恒成立,只需要△<0即可,
∴△36a2-36(a2-2a-6)<0,
解得:a<-3
∴此时a无解,此情况不存在;
当$\frac{a}{3}$≥$\frac{1}{3}$时,
即:a≥1,
此时函数y在-$\frac{1}{3}$≤x≤$\frac{1}{3}$上,y随着x的增大而减少,
∴x=$\frac{1}{3}$,y=a2-4a-5>0,
∴a<-1或a>5
∴a>5
综上所述,a<-$\sqrt{5}$或a>5时,-$\frac{1}{3}$≤x≤$\frac{1}{3}$时,y>0恒成立,
故答案为:a<-$\sqrt{5}$或a>5
点评 本题考查二次函数的性质,解题的关键是熟练运用二次函数的图象,本题属于中等题型.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 打开电视,它正在播广告是必然事件 | |
| B. | 要考察一个班级中的学生对建立生物角的看法适合用抽样调查 | |
| C. | 在抽样调查过程中,样本容量越大,对总体的估计就越准确 | |
| D. | 甲、乙两人射中环数的方差分别为S甲2=2,S乙2=4,说明乙的射击成绩比甲稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
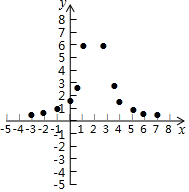 有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.
有这样一个问题:探究函数y=$\frac{6}{(x-2)^{2}}$的图象与性质.| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | 1 | 3 | $\frac{7}{2}$ | 4 | 5 | 6 | 7 | … |
| y | … | $\frac{6}{25}$ | $\frac{3}{8}$ | $\frac{2}{3}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | 6 | 6 | $\frac{8}{3}$ | $\frac{3}{2}$ | $\frac{2}{3}$ | $\frac{3}{8}$ | m | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{a+1}{a+2}$ | C. | $\frac{a+1}{a}$ | D. | $\frac{a}{a+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | π-3.14=0 | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | a3÷a=a2 | D. | a•a=2a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5×105 | B. | 2.5×106 | C. | 2.5×10-5 | D. | 2.5×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.
如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com