
分析 (1)直接利用积的乘方运算法则化简进而利用单项式乘以单项式求出答案;
(2)直接利用多项式除法运算法则求出答案;
(3)直接利用平方差公式以及完全平方公式化简求出答案;
(4)直接利用平方差公式以及完全平方公式化简,进而求出答案.
解答 解:(1)$\frac{1}{2}{a^2}b{c^3}•{(-2{a^2}{b^2}c)^2}$
=$\frac{1}{2}$a2bc3•(4a4b4c2)
=2a6b5c5;
(2)(25m2+15m3n-20m4)÷(-5m2)
=-5-3mn+4m2;
(3)(2a+3b)(2a-3b)-(a-3b)2
=4a2-9b2-(a2+9b2-6ab)
=3a2-18b2+6ab;
(4)(x+2y)2-(x+y)(x-y),
=x2+4y2+4xy-(x2-y2)
=5y2+4xy
把$x=-2,y=\frac{1}{2}$代入上式得:
原式=5×$\frac{1}{4}$+4×(-2)×$\frac{1}{2}$
=-$\frac{11}{4}$.
点评 此题主要考查了整式的混合运算以及化简求值,正确应用乘法公式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
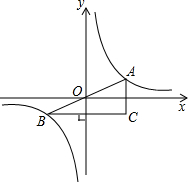 如图,A、B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴.
如图,A、B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个分支关于原点成中心对称 | B. | 两个分支分布在第二、四象限 | ||
| C. | 两个分支关于x轴成轴对称 | D. | 必经过点(1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com