
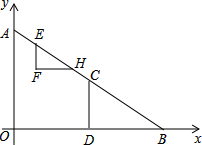
 已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒).
已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒).分析 (1)作EM⊥OA垂足为M,由△EFH∽△AOB,得$\frac{EF}{AO}$=$\frac{EH}{AB}$,可以求出EH,由EM∥OB,得$\frac{AM}{AO}$=$\frac{EM}{OB}$=$\frac{AE}{AB}$,可以解决点F坐标.
(2)根据AE+EH=AC,列出方程即可解决.
(3)分三种情形:①如图2中,FH与CD交于点M,当$\frac{15}{8}$≤t$≤\frac{15}{4}$时,②如图3中,$\frac{15}{4}$<t≤5时,S=S△CDB=6,③如图4中,当5<t≤10时,画出图象求出重叠部分面积即可.
(4)如图5中,在整个运动过程中Rt△EFH扫过的面积=S△AFH=$\frac{1}{2}$•FH•(AO+BF),由此即可计算.
解答 解:(1)如图1中,作EM⊥OA垂足为M,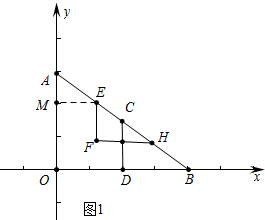
∵AE=EF=t,AO=6,BO=8,∠AOB=90°,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
∵∠AOB=∠EFH=90°,∠EHF=∠ABO,
∴△EFH∽△AOB,
∴$\frac{EF}{AO}$=$\frac{EH}{AB}$,即$\frac{t}{6}$=$\frac{EH}{10}$,
∴EH=$\frac{5}{3}$t,
∵EM∥OB,
∴$\frac{AM}{AO}$=$\frac{EM}{OB}$=$\frac{AE}{AB}$,
∴AM=$\frac{3}{5}$t,EM=$\frac{4}{5}$t,
∴点F坐标($\frac{4}{5}$t,6-$\frac{8}{5}$t).
故答案分别为:t,$\frac{5}{3}$t,$\frac{4}{5}$t,6-$\frac{8}{5}$t.
(2)如图2中,当点H与点C重合时,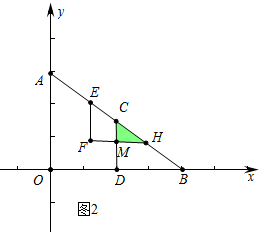
AE+EH=AC,
∴t+$\frac{5}{3}$t=5,
∴t=$\frac{15}{8}$,
∴t=$\frac{15}{8}$时,点H与点C重合.
(3)当点H与点B重合时,AE+EH=AB,
∴t+$\frac{5}{3}$t=10,
∴t=$\frac{15}{4}$,
当点E与点C重合时,t=5,
当点E与点B重合时,t=10,
①如图2中,FH与CD交于点M,当$\frac{15}{8}$≤t$≤\frac{15}{4}$时,
∵CH=EH-EC=EH-(AC-AE)=$\frac{5}{3}$t-5+t=$\frac{8}{3}$t-5.CM=$\frac{3}{5}$CH=$\frac{8}{5}$t-3,MH=$\frac{4}{5}$CH=$\frac{32}{15}$t-4,
∴S=$\frac{1}{2}$•CM•MH=$\frac{1}{2}$($\frac{8}{5}$t-3)($\frac{32}{15}$t-4)=$\frac{128}{75}$t2-$\frac{32}{5}$t+6.
②如图3中,$\frac{15}{4}$<t≤5时,S=S△CDB=6,
③如图4中,当5<t≤10时,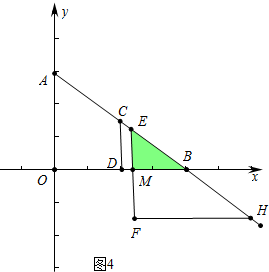
∵EB=AB-AE=10-t,EM=$\frac{3}{5}$EB=6-$\frac{3}{5}$t,BM=$\frac{4}{5}$EB=8-$\frac{4}{5}$t,
∴S=$\frac{1}{2}$•EM•MB=$\frac{1}{2}$•(6-$\frac{3}{5}$t)(8-$\frac{4}{5}$t)=$\frac{6}{25}$(10-t)2.
综上所述:S=$\left\{\begin{array}{l}{\frac{128}{75}{t}^{2}-\frac{32}{5}t+6}&{(\frac{15}{8}≤t≤\frac{15}{4})}\\{6}&{(\frac{15}{4}<t≤5)}\\{\frac{6}{25}(10-t)^{2}}&{(5<t≤10)}\end{array}\right.$.
(3)如图5中,在整个运动过程中Rt△EFH扫过的面积=S△AFH=$\frac{1}{2}$•FH•(AO+BF)=$\frac{1}{2}$•$\frac{40}{3}$•16=$\frac{320}{3}$.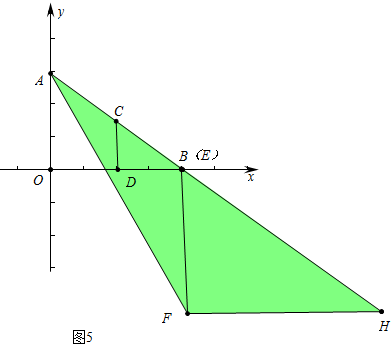
点评 本题考查三角形综合题、相似三角形的判定和性质,勾股定理、分段函数等知识,解题的关键是正确画出图象,学会分类讨论的思想,应用的知识比较多,属于中考压轴题.


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
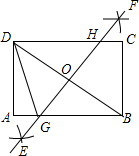 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )| A. | $\frac{25}{8}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:
已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A、B两地相距80km,甲、乙二人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DB、OC分别表示表示甲、乙二人离开A地距离S(km)与时间t(h)的函数关系,根据题中的图象填空:
已知A、B两地相距80km,甲、乙二人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DB、OC分别表示表示甲、乙二人离开A地距离S(km)与时间t(h)的函数关系,根据题中的图象填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com