
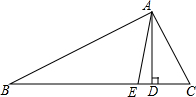
 如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.
如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.分析 (1)根据三角形的内角和定理,可求得∠BAC的度数,由AD是∠BAC的平分线,可得∠DAC的度数;在直角△AEC中,可求出∠EAC的度数,所以∠DAE=∠DAC-∠EAC,即可得出;
(2)与(1)解法相同,只是把度数换成角即可.
解答 解:∵△ABC中,∠B=28°,∠C=66°,
∴∠BAC=180°-∠B-∠C=180°-28°-66°=86°,
∵AE是∠BAC的平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=43°,
∵AD是BC边上的高,
在直角△ADC中,
∵∠DAC=90°-∠C=90°-66°=24°,
∴∠DAE=∠EAC-∠DAC=43°-24°=19°;
(2)∵△ABC中,∠BAC=180°-∠B-∠C,
∵AE是∠BAC的平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C),
∵AD是BC边上的高,
在直角△ADC中,
∵∠DAC=90°-∠C,
∴∠DAE=∠EAC-∠DAC═$\frac{1}{2}$(180°-∠B-∠C)-(90°-∠C)=$\frac{1}{2}$(∠C-∠B)
点评 本题考查的是三角形的内角和定理,三角形的高、角平分线的性质,学生应熟练掌握三角形的高、中线和角平分线这些基本知识,能灵活运用解决问题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图(保留作图痕迹,不需写作法)并计算:
作图(保留作图痕迹,不需写作法)并计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.
在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
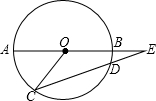 如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com