
分析 根据等边三角形的性质,①最长的面径是等边三角形的高线;②最短的面径平行于三角形一边,最长的面径为等边三角形的高,然后根据相似三角形面积的比等于相似比的平方求出最短面径.
解答 解:如图,
①等边三角形的高AD是最长的面径,
AD=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$;
②当EF∥BC时,EF为最短面径,
此时,($\frac{EF}{BC}$)2=$\frac{1}{2}$,
即$\frac{EF}{4}$=$\frac{\sqrt{2}}{2}$,
解得EF=2$\sqrt{2}$.
所以,它的面径长2$\sqrt{2}$≤x≤2$\sqrt{3}$
故答案为:2$\sqrt{2}$≤x≤2$\sqrt{3}$.
点评 本题考查了等边三角形的性质,读懂题意,弄明白面径的定义,并准确判断出等边三角形的最短与最长的面径是解题的关键.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
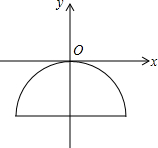 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.
如图,在平面直角坐标系中,直线y=kx+5与x轴交于点A,与y交于点B,与抛物线y=ax2+bx交于点C、D.已知点C坐标为(1,7),点C横坐标为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
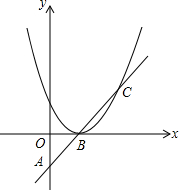 如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.
如图,抛物线y=ax2沿着x轴移动,与直线AB相交于B,C两点,若B(1,0)且OA=OB,AB=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
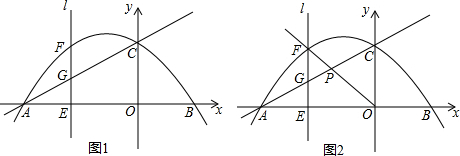
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2})^{2}=-\frac{1}{4}$ | B. | 3a-2=$\frac{1}{3{a}^{2}}$ | C. | (-1)0=1 | D. | 00=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com