
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
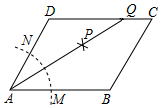 如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为15.
如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为15.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,…,依此规律,点A2017的坐标是(21008,21008).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
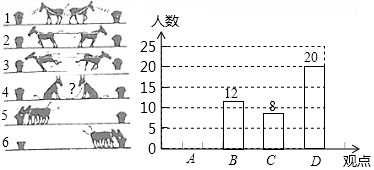 主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:| 观点 | 频数 | 频率 |
| A | a | 0.2 |
| B | 12 | 0.24 |
| C | 8 | b |
| D | 20 | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
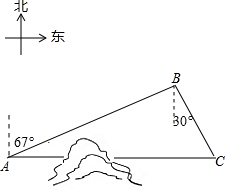 如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
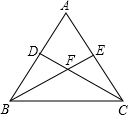 如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com