
����Ŀ��ij�̳�����һ�ֳɱ�Ϊÿ��60Ԫ�ķ�װ���涨�����ڼ����۵��۲����ڳɱ����ۣ��һ������ø���45%�����������֣�������![]() �����������۵���
�����������۵���![]() ��Ԫ������һ�κ���
��Ԫ������һ�κ���![]() ����
����![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��1����һ�κ���![]() �ı���ʽ��
�ı���ʽ��
��2�������̳��������Ϊ![]() Ԫ����д������
Ԫ����д������![]() �����۵���
�����۵���![]() ֮��Ĺ�ϵʽ�����۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
֮��Ĺ�ϵʽ�����۵��۶�Ϊ����Ԫʱ���̳��ɻ�����������������Ƕ���Ԫ��
��3�������̳����������500Ԫ����ȷ�����۵���![]() �ķ�Χ��
�ķ�Χ��
���𰸡��⣺��1��һ�κ����ı���ʽΪ![]()
��2�������۵��۶�Ϊ87Ԫʱ���̳��ɻ������������������891Ԫ
��3�����۵���![]() �ķ�Χ��
�ķ�Χ��![]() ��
��
��������
���⣨1���г���Ԫһ�η�������k��b��ֵ�����һ�κ����ı���ʽ��
��2�����������W��x�ĺ�������ʽ���Ƴ���x=87ʱ�̳��ɻ���������
��3����w=500�Ƴ�x2��180x+7700=0���x��ֵ���ɣ�
�����������1����������ã�![]() �����k=��1��b=120������һ�κ����ı���ʽΪ
�����k=��1��b=120������һ�κ����ı���ʽΪ![]() ��
��
��2��![]() =
=![]() ���������ߵĿ������£�����x��90ʱ��W��x��������������۵��۲����ڳɱ����ۣ��һ������ø���45%����60��x��60����1+45%������60��x��87������x=87ʱ��W=
���������ߵĿ������£�����x��90ʱ��W��x��������������۵��۲����ڳɱ����ۣ��һ������ø���45%����60��x��60����1+45%������60��x��87������x=87ʱ��W=![]() =891���������۵��۶�Ϊ87Ԫʱ���̳��ɻ������������������891Ԫ��
=891���������۵��۶�Ϊ87Ԫʱ���̳��ɻ������������������891Ԫ��
��3����![]() =500���ⷽ��
=500���ⷽ��![]() ��
��![]() ���
���![]() ��
��![]() ������60��
������60��![]() ��87 �����Ե�
��87 �����Ե�![]() ��500ʱ��70��
��500ʱ��70��![]() ��87��
��87��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���P��BC����һ���㣬����AP��AP�Ĵ�ֱƽ���߽�BD�ڵ�G���� AP�ڵ�E����P����B�㵽C����˶������У���APG�Ĵ�С�仯�����( )

A. ��� B. �ȱ����С C. �ȱ�С���� D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������²���ʵ�飬��һ����40 cm����˿�������Σ�����ÿ����β������Χ��һ�������Σ�
(1)Ҫʹ�����������ε����֮�͵���58 cm2������Ӧ����ô�������˿��
(2)������Ϊ�����������ε����֮�Ͳ����ܵ���48 cm2������Ϊ����˵����ȷ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�е�![]() �ͣ������Σ���
�ͣ������Σ���![]() �ͣ����Σ���
�ͣ����Σ���![]() �ͣ�����ֱ�������Σ�ֽƬ�ֱ����
�ͣ�����ֱ�������Σ�ֽƬ�ֱ����![]() �������У����ӵ���״����С���ʵض���ͬ���ٽ���
�������У����ӵ���״����С���ʵض���ͬ���ٽ���![]() ������װ��һֻ�����Ĵ����У�
������װ��һֻ�����Ĵ����У�
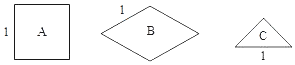
��1�����Ⱥ��������![]() �����ӣ����е�ֽƬ������Գ�ͼ���������ĶԳ�ͼ�εĸ������� ����
�����ӣ����е�ֽƬ������Գ�ͼ���������ĶԳ�ͼ�εĸ������� ����
��2�����Ⱥ��ȴ�������![]() �����ӣ����Żأ����ٴ����µ�
�����ӣ����Żأ����ٴ����µ�![]() ������������
������������![]() �����ӣ���������
�����ӣ���������![]() �����е�ֽƬ������ȵı�ƴ��һ����ƴ�ɵ�ͼ������Գ�ͼ�εĸ��ʣ������ص���϶ƴ�ӣ�
�����е�ֽƬ������ȵı�ƴ��һ����ƴ�ɵ�ͼ������Գ�ͼ�εĸ��ʣ������ص���϶ƴ�ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������սʿ����ͬ�����¸����10�Σ�ÿ�����еĻ����ֱ��ǣ�
�ף�8��6��7��8��6��5��9��10��4��7 �ң�6��7��7��6��7��8��7��9��8��5
��1���ֱ�����������ݵķ���ͱ��
��2�����ݼ�����������һ������սʿ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η�����
��һԪ���η�����![]() .
.
(1)��֤����������ʵ��![]() �����̶���ʵ������
�����̶���ʵ������
(2)��![]() Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
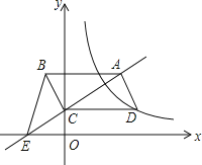
����Ŀ����ͼ��ƽ���ı���ABCD�Ķ���C��y���������ϣ�CDƽ����x�ᣬֱ��AC��x���ڵ�E��BC��AC������BE������������![]() (x��0)��ͼ����D����֪S��BCE=1����k=______��
(x��0)��ͼ����D����֪S��BCE=1����k=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����������ۼ�����S����Ԫ����ʱ��t���£�֮��Ĺ�ϵ����ǰt���µ������ܺ�S��t֮��Ĺ�ϵ��Ϊ���κ�����ϵ���Ը���ͼ���ṩ����Ϣ������������⣺
��1�����ۼ�����S����Ԫ����ʱ��t���£�֮��ĺ�������ʽ��
��2����������ĩ�ù�˾�ۼ�����ɴ�16��Ԫ��
��3����10���¸ù�˾���������Ƕ�����Ԫ��
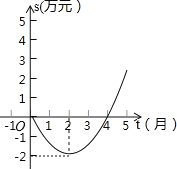
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �뷴��������
�뷴��������![]() �ڵ�һ�����ڵ�ͼ���ཻ�ڵ�
�ڵ�һ�����ڵ�ͼ���ཻ�ڵ�![]() .
.
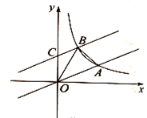
��1�����������Ľ���ʽ��
��2����ֱ��![]() ����ƽ�ƺ��뷴��������ͼ���ڵ�һ�����ڽ��ڵ�
����ƽ�ƺ��뷴��������ͼ���ڵ�һ�����ڽ��ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����ֱ��
����ֱ��![]() �Ľ���ʽ.
�Ľ���ʽ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com