
| A. | $\sqrt{13}$ | B. | 6$\sqrt{2}$+2$\sqrt{3}$ | C. | 6$\sqrt{2}$+4$\sqrt{3}$ | D. | 以上答案都不对 |
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
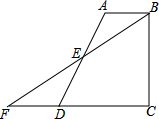 如图,在四边形ABCD中,AB∥CD,BC⊥CD,垂足为点C,E是AD的中点,连接BE并延长交CD的延长线于点F.
如图,在四边形ABCD中,AB∥CD,BC⊥CD,垂足为点C,E是AD的中点,连接BE并延长交CD的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
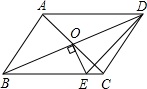 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长是多少?
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E,若△CDE的周长为10,则平行四边形ABCD的周长是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com